Soil Hydraulic Properties DATABASE of the Pampas Region in Buenos Aires Province

BASE de DATOS de Propiedades hidráulicas del suelo de la región pampeana de la provincia de Buenos Aires

Aile Selenne Golin ⁽¹⁾, Claudio Ramón Mujica ⁽²⁾ & Ignacio Villanueva ⁽³⁾

⁽¹⁾ Instituto de Hidrología de Llanuras “Dr. Eduardo Jorge Usunoff” & Universidad Nacional del Centro de la Provincia Buenos Aires, Azul, Argentina.

e-mail: ailegolin@gmail.com. ORCID: https://orcid.org/0009-0008-9406-8642

⁽²⁾ Instituto de Hidrología de Llanuras “Dr. Eduardo Jorge Usunoff” & Universidad Nacional del Centro de la Provincia Buenos Aires, Azul, Argentina.

e-mail: cmujica@ihlla.org.ar. ORCID: https://orcid.org/0000-0002-2379-1955

⁽³⁾ Instituto de Hidrología de Llanuras “Dr. Eduardo Jorge Usunoff” & Universidad Nacional del Centro de la Provincia Buenos Aires, Azul, Argentina.

e-mail: ivillanueva@ihlla.org.ar. ORCID: https://orcid.org/0000-0002-6951-2114

ABSTRACT

Flatland areas, such as the Pampas in South America, rank among the world’s most economically productive landscapes. Over the last century, these regions have been increasingly used for intensive production, which has resulted in significant environmental impacts. These include alterations in pH, salinity, and other soil properties; changes in water flows and balances; increased floods and droughts; and heightened wind and water erosion. To address these challenges, numerical process-based models are essential to assess the highly variable, interconnected, and nonlinear processes that drive these impacts. Such models rely on comprehensive soil databases including hydraulic properties to provide representative results. This study aimed to develop a robust database of soil properties for the Buenos Aires Province in Argentina, encompassing much of the Pampas region. Using granulometric and physicochemical data from the Instituto Nacional de Tecnología Agropecuaria (INTA) database, we applied 38 pedotransfer functions to 381 soil profiles to estimate hydraulic parameters. These were compared with seven calibrated parameter sets from the different study sites. This study demonstrated that model performance varies depending on the evaluated function, with specific models excelling in particular variables, highlighting the need for careful selection based on the characteristics of the dataset.

Keywords: INTA, Robust Soil Database, Pedotransfer Functions, Unsaturated Flow, Productive Flatlands.

RESUMEN

Las llanuras, como la Pampa en Sudamérica, se encuentran entre los paisajes más productivos del mundo. En el último siglo, estas regiones han sido intensamente explotadas para actividades agrícolas, generando impactos ambientales significativos, como alteraciones del pH y la salinidad del suelo, cambios en los flujos hídricos, aumento de inundaciones y sequías, y mayor erosión eólica e hídrica. Para abordar estos desafíos, los modelos numéricos basados en procesos son fundamentales para evaluar las interacciones complejas y no lineales que los impulsan. Estos modelos requieren bases de datos detalladas de propiedades del suelo, incluidas las hidráulicas. Este estudio desarrolló una base de datos de propiedades del suelo para la provincia de Buenos Aires (Argentina), que comprende gran parte de la región pampeana. A partir de datos granulométricos y fisicoquímicos del Instituto Nacional de Tecnología Agropecuaria (INTA), se aplicaron 38 funciones de pedotransferencia a 381 perfiles de suelo para estimar parámetros hidráulicos, comparándolos con siete conjuntos calibrados en siete sitios. Los resultados evidenciaron que el desempeño de las funciones varía según la variable evaluada, destacando la importancia de seleccionar modelos específicos según las características del conjunto de datos.

Palabras clave: INTA, Base de Datos de Suelos Robusta, Funciones de Pedotransferencia, Flujo No Saturado, Llanuras Productivas.

INTRODUCTION

The Argentine Pampa is the largest sedimentary loess plain in South America and includes the province of Buenos Aires, the largest in the country at 307571 km². This region, part of the Rio de la Plata grasslands, is characterized by shallow soils, salinity, and frequent floods and droughts, which limit agriculture and preserve extensive natural grasslands. Despite these challenges, it remains one of the most economically productive areas (Golin et al., 2024; Mujica et al., 2021; Jobbágy & Jackson, 2007).

Intensified land use has significantly impacted soil properties (pH, salinity) and water balance, leading to more frequent floods, droughts, and erosion. These changes disrupt the hydrological cycle by reducing the soil's ability to retain moisture, which is vital for plant growth, ecosystem stability, and flood prevention (Mujica et al., 2019; Damiano & Taboada, 2000). Understanding soil water flow and plant uptake is crucial for addressing these (Sun et al., 2024).

The complex nature of environmental systems in the Pampas requires the use of process-based numerical models to predict the effects of land use changes. These models depend on accurate data on soil hydraulic properties. However, obtaining these parameters by direct measurement is often costly and challenging. As a result, pedotransfer functions (PTFs) are often used to estimate these properties using more readily available information. PTFs have been shown to be effective in improving the accuracy of hydrological models and improving the prediction of groundwater and surface runoff processes (Zimmermann & Basile, 2011).

The accuracy of numerical models relies on the quality of the soil property databases. Key parameters, such as field capacity, bulk density, and residual and saturated water content, are essential for accurately modeling water and solute fluxes. Global databases, such as UNSODA 2.0, and regional databases, such as those of INTA in Argentina, are valuable for predicting phenomena such as runoff and infiltration, as well as for the sustainable management of water resources (Zimmermann & Basile, 2007, 2008).

OBJECTIVES

The objective of this study was to develop a robust database of soil properties for the province of Buenos Aires, Argentina, located in the Pampas region, with the aim of obtaining the most accurate estimation of hydraulic properties for soil profiles across each cartographic unit in 1:50000 scale soil maps of the province (Figure 1). This was achieved by digitizing and organizing the soil series data provided by INTA into structured tables representing the proportions of cartographic units in the soil maps. The focus was on estimating hydraulic properties, such as water retention and soil permeability, from granulometric and physicochemical data, which are essential for modeling soil-water interactions.

The estimated hydraulic properties were validated against seven calibrated points, enabling the selection of the most reliable pedotransfer functions for this region.

METODOLOGY

Study area

Buenos Aires Province's heterogeneity is determined by geomorphological, edaphic, climatic, and phytogeographical differences, which allowed the delimitation of sub-regions (Oyarzabal et al., 2018). Land is extremely flat, with slopes ranging from < 0.1 to 5%, and they are naturally covered by temperate grasslands (Soriano, 1992). The average annual rainfall ranges from ~ 600 to ~ 1000 mm, and the average annual temperature ranges from ~ 14°C to ~ 17°C. (Podestá et al., 1999). This region is distinguished by a moisture gradient that extends from east to west, along with increasing continental characteristics as one moves towards the northwest (Burgos & Vidal, 1951).

The dominant soils in the region are mollisols from the Late Pleistocene-Holocene sediments (Zárate, 2003; Teruggi, 1957). The low-gradient relief leads to minimal runoff, with water primarily eliminated through evapotranspiration (Lavado & Taboada, 2009; Varni & Usunoff, 1999), resulting in recurrent flooding, increasing salinity, and decreasing the water table depth (Jobbágy et al., 2017; Barranquero et al., 2012). In the Pampa Ondulada region, the landscape features gentle ondulations drained by the Paraná and the Río de la Plata tributaries. Soils consist of clayey loess with low sand content (< 5%) and high silt content (~ 70%), with grain size decreasing from SW to NE (Zárate & Tripaldi, 2012; Zárate, 2003).

The Flat Interior Pampa has a gentle relief of eolian dunes that control its poorly integrated surface drainage and coarse-grained textured soils. The Western Interior Pampa is a low-relief plain drained by ephemeral streams and the Quinto River and presents a complex pattern of dunes formed by fine sand and silt sediments (Zárate & Tripaldi, 2012).

The Pampa Deprimida consists of a very flat terrain that developed from the same loessic sediments, contains more sands towards the southwest, and also has inputs of silty sediments. The deposition of these sediments traced longitudinal formations several kilometers long, 1-1.5 m high and a few hundred meters wide, as well as parabolic dunes adjacent to deflation basins. In Pampa Austral (also known as Pampa Interserrana), loessic deposits form a continuous blanket over the large and complex sandy dune systems of central Argentina. The sediments that form this sub-region are coarser and are commonly classified as sandy, silty clayey loams, although sites with finer textured soils and petrocalcic horizons can be found that are heterogeneous with varying degrees of cementation and thickness (Zárate & Tripaldi, 2012; Zárate, 2003).

Soil charts

In this study, we utilized vector-based soil data provided by the Instituto Nacional de Tecnología Agropecuaria (National Institute of Agricultural Technology, INTA) for Buenos Aires Province on a 1:50000 scale (INTA, 2022). This dataset was derived from the digitization of the original Soil Charts of the Argentine Republic, which were developed as part of the Plan Mapa de Suelos de la Región Pampeana initiated in 1964. This project marked a significant advancement in national soil classification efforts, focusing on semi-detailed and reconnaissance-level mapping (1:50000–1:100000). The data offers comprehensive information on soil series and is publicly available.

To process these data, Python scripts were developed to extract and parse field data from PDF files containing information on 381 soil series (out of a total of 383, two of which were unreadable) in Buenos Aires Province. These scripts converted the extracted data into a structured format and organized them into Python dictionaries for ease of further analysis. The resulting robust database includes hydraulic parameters estimated using pedotransfer functions, as detailed in Table 1. This digital database is now ready for integration into hydrological and soil modeling applications.

Calibrated control points

The data considered as observed were obtained from two doctoral thesis from the “Dr. Eduardo Usunoff” Instituto de Hidrología de Llanuras (IHLLA). In Mujica (2020), the measurements were performed as follows:

The textural class of each horizon was obtained using the hydrometer method (Bouyoucos, 1962), whereas bulk density was found by weighing samples of undisturbed soil cylinders (169.65 cm³, after drying them for 24 h at 105°C). In addition, pH and electrical conductivity (EC) were measured on samples corresponding to each of the horizons. These measurements were performed on the supernatant of dilutions with a soil: water ratio of 1:2.5, previously shaken (6 h), using an OAKTON PC700 reader with a pH probe Cole-Palmer 05992-62 and EC-temperature probe 35608-74 (Chapter 3). The parameters for the van Genuchten model (van Genuchten, 1980) were calibrated using the MIN3P model (Bea et al., 2012; Mayer et al., 2002) from hydrological data measured in the study plots (continuous soil moisture, transpiration, precipitation, and soil temperature).

Weinzettel (2005) obtained the parameters in the field as follows:

In the superficial part of the soil, a tension infiltration meter was used specially to evaluate certain hydraulic parameters of the soil, such as the saturated hydraulic conductivity and the hydraulic conductivity at different tensions close to saturation, as well as to evaluate the presence of soil macroporosity. It was also used to evaluate the presence of soil macroporosity (Chapter 3).

To obtain the K(θ) functions of each plot, internal drainage tests or instantaneous profile method (Hillel et al., 1972). The test requires periodic measurements of moisture and hydraulic potential at different depths while water drains from the previously saturated soil, without evapotranspiration (Chapter 4).

Points used for calibration (Longitude, Latitude, INTA Soil Series): P1 (-57.83°, -36.1°, Los Naranjos), P2 (-58.906°, -37.498°, Tandil), P3 (-0.063°, -37.155°, Mar del Plata), P4 (-59.654°, -36.947°, Tandil) (Mujica, 2020); P5 (-59.883°, -36.767°, Gral. Guido), P6 (-59.866°, -36.622°, Blanca Chica), P7 (-59.93°, -37.001°, Mar del Plata) (Weinzettel, 2005).

Quantitative Evaluation

The data from the seven calibration sites encompassing all depths were grouped by calculated variables: bulk density (ρ_b), saturated conductivity (K_s), van Genuchten model exponent (n) and the alpha parameter of soil water retention (α), the saturated water content (θ_s), the residual water content (θ_r), wilting point (θ₁₅₀₀), and field capacity (θ₃₃); classified according to the functions utilized as shown in Table 1 and the Rosetta model, that implements artificial neural network for five PTFs in a so-called hierarchical approach. Rosetta model estimates K_s, n and α (Schaap, 2004), was implemented through a Python package (Skaggs, n.d.) which was executed twice. First, using the parameters ρ_b, θ₁₅₀₀, and θ₃₃ obtained through the formulas of Rawls (Rawls et al., 2004), and second, using those derived from Saxton's formulas (Saxton & Rawls, 2006).

For each group, residuals were computed, and statistical metrics such as standard deviation, Pearson’s correlation coefficient, and reference standard deviation (based on observed values) were calculated. The analysis employed the geometric relationships illustrated in the Taylor Diagram, which visually integrates these metrics, enabling a comprehensive evaluation of the model performance and the development of balanced skill scores that capture multiple dimensions of accuracy (Taylor, 2001).

RESULTS AND DISCUSSION

The evaluation of model performance across variables revealed significant variability. For the ρ_b, 64 modeled values and 32 observed values were analyzed. The observed standard deviation (0.2626) exceeded those modeled by Saxton (0.1555) and Rawls (0.1167), which also showed low correlations of 0.1091 and 0.4673, respectively. Rawls performed the best (Figure 2). For Ks, none of the models captured observed variability (60.2092). A total of 436 modeled values and 31 observed values were analyzed. Among them, Saxton and Vereecken (Vereecken et al., 1990) achieved the highest correlations (0.5865 and 0.4606, respectively) but underestimated the standard deviation (18.0016 and 10.8391, respectively), Saxton performed the best (Figure 3). For the 87 calculated values and 25 measured values of the parameter n, only Rawls and Brakensiek (Rawls and Brakensiek, 1989) exceeded the observed standard deviation (0.1051) with a value of 0.3123, although it showed a low correlation of 0.1232. The other models demonstrated correlations below 0.2, and performed similar and better (Figure 4). For the 137 calculated values and 31 observed values of the parameter α, Wösten et al. (1999) and Vereecken produced the highest correlations (0.1349 and 0.1868, respectively), although their standard deviations deviated considerably from the observed value (0.0050), Wösten performed the worst and Vereecken the best (Figure 5). For θs, Wösten demonstrated the strongest correlation (0.5165), followed by Vereecken (0.4386), despite neither replicating the observed variability (0.1262). The analysis was based on 144 calculated values and 32 observed values, all models with similar performance, and Rosetta Saxton the worst (Figure 6). For θr, Rosetta Saxton demonstrated the strongest correlation (0.4117), followed by Rosetta Rawls (0.4067), despite neither replicating the observed variability (0.0599). The analysis was based on 160 calculated values and 32 observed values, both Rosetta performed the best (Figure 7). For θ₃₃, both Saxton and Rawls achieved standard deviations (6.0028 and 1.6959, respectively) closer to the observed value (15.1958) but exhibited weak correlations (0.0199 and 0.2574, respectively). The analysis included 64 calculated values and 32 observed values; Rawls performed better than Saxton (Figure 8). Lastly, for θ₁₅₀₀, Saxton and Rawls demonstrated comparable correlations (0.2982 and 0.2988, respectively) and standard deviations (6.2997 and 5.6546, respectively) that were close to the observed variability (7.6369). This analysis also included 64 calculated values and 32 observed values, Rawls performed better than Saxton (Figure 9). Overall, the analysis underscores substantial differences in model performance, with specific models excelling in certain metrics, but none achieving a comprehensive representation across all variables. It should be noted that here we are evaluating a set of pedotransfer functions applied to a coarse soil dataset (INTA Soil Series) against in situ data, so high accuracy of results can't be expected. On the other hand, the INTA soil series data are very valuable for the application of hydrological modelling where soil data are not available.

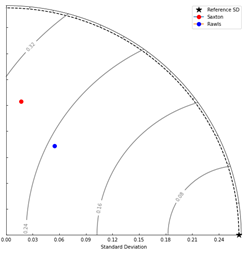
Figure 2. ρ_bmodel performance at 7 locations across all depths.

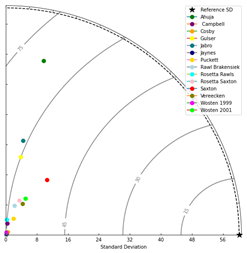
Figure 3. K_s model performance at 7 locations across all depths.

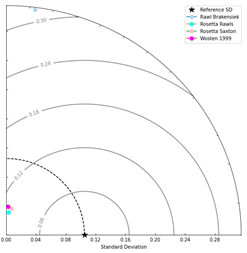
Figure 4. n model performance at 7 locations across all depths.

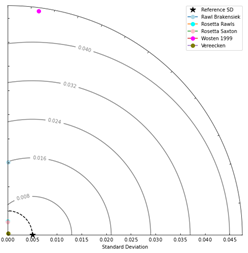
Figure 5. α model performance at 7 locations across all depths.

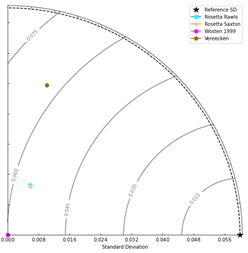
Figure 7. θ_r model performance at 7 locations across all depths.

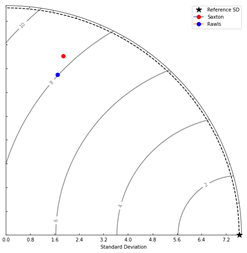
Figure 9. θ₁₅₀₀model performance at 7 locations across all depths.

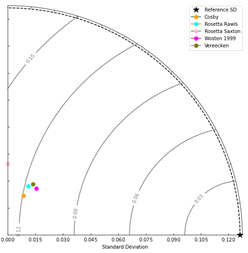
Figure 6. θ_s model performance at 7 locations across all depths.

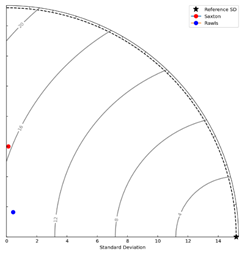
Figure 8. θ₃₃model performance at 7 locations across all depths.

CONCLUSIONS

The results show that the models evaluated have difficulty fully replicating the observed variability in the variables. In most cases, low Pearson correlation coefficients (r) indicate a weak relationship between the modeled and observed values, which limits the predictive accuracy of the models. Taylor diagrams are a powerful tool for visually assessing statistical metrics that quantify model performance and have been key in evaluating models by comparing their ability to replicate observed variability.

This study could benefit from an increase in observed measurements, which would improve the evaluation tools and provide greater robustness to the analysis. In summary, the model selection should be based on the specific performance of each model for each variable, adjusting the choice according to the particular characteristics of the variables.

ACKNOWLEDGEMENTS

We express our deep gratitude to the “Dr. Eduardo Jorge Usunoff” Instituto de Hidrología de Llanuras (IHLLA) and the Consejo Nacional de Investigaciones Científicas y Técnicas (CONICET) for their invaluable support throughout this research.

REFERENCES

Ahuja, L. R., Cassel, D. K., Bruce, R. R. & Barnes, B. B. (1989). Evaluation of spatial distribution of hydraulic conductivity using effective porosity data. Soil Science, 148(6), 404–411. https://doi.org/10.1097/00010694-198912000-00002

Barranquero, R. S., Varni, M., Ruiz de Galarreta, A. & Banda Noriega, R. (14-15 de junio de 2012). Evaluación de las características del agua subterránea en la cuenca del arroyo Langueyú, Tandil, Buenos Aires, Argentina. 1er Encuentro de investigadores en Formación en Recursos Hídricos. Ezeiza, Buenos Aires, Argentina. https://www.researchgate.net/publication/319621092_Evaluacion_de_las_caracteristicas_del_agua_subterranea_en_la_cuenca_del_arroyo_Langueyu_Tandil_Buenos_Aires_Argentina

Bea, S. A., Wilson, S. A., Mayer, K. U., Dipple, G. M., Power, I. M. & Gamazo, P. (2012). Reactive Transport Modeling of Natural Carbon Sequestration in Ultramafic Mine Tailings. Vadose Zone Journal, 11(2), vzj2011.0053. https://doi.org/10.2136/vzj2011.0053

Bouyoucos, G. J. (1962). Hydrometer Method Improved for Making Particle Size Analyses of Soils¹. Agronomy Journal, 54(5), 464–465. https://doi.org/10.2134/agronj1962.00021962005400050028x

Burgos, J. J. & Vidal, A. L. (1951). The Climates of the Argentine Retublic According to the New Thornthmaite Classification. Annals of the Association of American Geographers, 41(3), 237–263. https://doi.org/10.1080/00045605109352055

Campbell, G. S. & Shiozawa, S. (1992). Prediction of hydraulic properties of soils using particle-size distribution and bulk density data. In M. T. Van Genuchten, F. J. Leij and L. J. Lund (Eds.), Indirect Methods for Estimating the Hydraulic Properties of Unsaturated Soils: Proceedings of the International Workshop on Indirect Methods for Estimating the Hydraulic Properties of Unsaturated Soils, Riverside, California, October 11-13, 1989 (pp. 317–328). U. S. Salinity Laboratory, Agricultural Research Service, U. S. Department of Agriculture. https://books.google.com.ar/books?id=smVRAAAAMAAJ

Cosby, B. J., Hornberger, G. M., Clapp, R. B. & Ginn, T. R. (1984). A Statistical Exploration of the Relationships of Soil Moisture Characteristics to the Physical Properties of Soils. Water Resources Research, 20(6), 682–690. https://doi.org/10.1029/WR020i006p00682

Damiano, F. & Taboada, M. A. (2000). Prediccion del agua disponible usando funciones de pedo-transferencia en suelos agricolas de la region pampeana. Ciencia del suelo 18(2), 77–88. https://suelos.org.ar/publicaciones/vol_18n2/damiano_77-88.pdf

Golin, A. S., Páez Campos, H. R., Guevara Ochoa, C., Dávila, C. F. & Vives, L. S. (2024). Assessing open-access digital elevation models for hydrological applications in a large scale plain: Drainage networks, shallow water bodies and vertical accuracy. Earth Surface Processes and Landforms, 49(15), 5269–5283. https://doi.org/10.1002/esp.6035

Gülser, C. & Candemir, F. (2008). Prediction of Saturated Hydraulic Conductivity Using Some Moisture Constants and Soil Physical Properties. Proceeding Balwois, 1–5. https://www.researchgate.net/profile/Coskun-Guelser/publication/228839205_Prediction_of_Saturated_Hydraulic_Conductivity_Using_Some_Moisture_Constants_and_Soil_Physical_Properties/links/0c96053b16981075ab000000/Prediction-of-Saturated-Hydraulic-Conductivity-Using-Some-Moisture-Constants-and-Soil-Physical-Properties.pdf

Hillel, D., Krentos, V. D. & Stylianou, Y. (1972). Procedure and test of an internal drainage method for measuring soil hydraulic characteristics in situ. Soil Science, 114(5), 395–400. https://doi.org/10.1097/00010694-197211000-00011

Instituto Nacional de Tecnología Agropecuaria (2022, May 26). El INTA digitaliza las cartas de suelos de la Provincia de Buenos Aires. INTA Informa. https://intainforma.inta.gob.ar/el-inta-digitaliza-las-cartas-de-suelos-de-la-provincia-de-buenos-aires/

Jabro, J. D. (1992). Estimation of saturated hydraulic conductivity of soils from particle size distribution and bulk density data. Transactions of the American Society of Agricultural and Biological Engineers, 35(2), 557–560. https://doi.org/10.13031/2013.28633

Jaynes, D. B. & Tyler, E. J. (1984). Using soil physical properties to estimate hydraulic conductivity. Soil Science, 138(4), 298–305. https://doi.org/10.1097/00010694-198410000-00007

Jobbágy, E. G. & Jackson, R. B. (2007). Groundwater and soil chemical changes under phreatophytic tree plantations. Journal of Geophysical Research: Biogeosciences, 112, G02013. https://doi.org/10.1029/2006JG000246

Jobbágy, E. G., Tóth, T., Nosetto, M. D. & Earman, S. (2017). On the Fundamental Causes of High Environmental Alkalinity (pH ≥ 9): An Assessment of Its Drivers and Global Distribution. Land Degradation & Development, 28(7), 1973–1981. https://doi.org/10.1002/ldr.2718

Lavado, R. S. & Taboada, M. A. (2009). The Argentinean Pampas: A key region with a negative nutrient balance and soil degradation needs better nutrient management and conservation programs to sustain its future viability as a world agroresource. Journal of Soil and Water Conservation, 64(5), 150A–153A. https://doi.org/10.2489/jswc.64.5.150A

Mayer, K. U., Frind, E. O. & Blowes, D. W. (2002). Multicomponent reactive transport modeling in variably saturated porous media using a generalized formulation for kinetically controlled reactions. Water Resources Research, 38(9), 1174. https://doi.org/10.1029/2001WR000862

Mujica, C. R. (2020). Modelación numérica de los cambios hidrogeoquímicos en la zona no saturada del suelo sometida a distintos usos primarios en la región centro-sur bonaerense [Tesis de doctorado, Facultad de Ciencias Agrarias y Forestales de la Universidad Nacional de La Plata]. https://doi.org/10.13140/RG.2.2.26412.62085

Mujica, C. R., Bea, S. A., Jobbágy, E. G. (2021). Modeling soil chemical changes induced by grassland afforestation in a sedimentary plain with shallow groundwater. Geoderma, 400(2021), 115158. https://doi.org/10.1016/j.geoderma.2021.115158

Mujica, C. R., Milione, G. M., Bea, S. A. & Jobbágy, E. G. (2019). Modelación de los cambios químicos en suelos inducidos por la forestación de pastizales naturales en ecosistemas de llanura. Ecología Austral, 29(3), 433–445. https://doi.org/10.25260/EA.19.29.3.0.896

Oyarzabal, M., Clavijo, J., Oakley, L., Biganzoli, F., Tognetti, P., Barberis, I., Maturo, H. M., Aragón, R., Campanello, P. I., Prado, D., Oesterheld, M. & León, R. J. C. (2018). Unidades de vegetación de la Argentina. Ecología Austral 28(1), 040–063. https://doi.org/10.25260/ea.18.28.1.0.399

Podestá, G. P., Messina, C. D., Grondona, M. O. & Magrin, G. O. (1999). Associations between Grain Crop Yields in Central-Eastern Argentina and El Niño–Southern Oscillation. Journal of Applied Meteorology, 38(1), 1488–1498. https://doi.org/10.1175/1520-0450(1999)038<1488:ABGCYI>2.0.CO;2

Puckett, W. E., Dane, J. H. & Hajek, B. F. (1985). Physical and Mineralogical Data to Determine Soil Hydraulic Properties. Soil Science Society of America Journal, 49(4), 831–836. https://doi.org/10.2136/sssaj1985.03615995004900040008x

Rawls, W. J. & Brakensiek, D. L. (1989). Estimation of Soil Water Retention and Hydraulic Properties. In H. J. Morel-Seytoux (Ed.), Unsaturated Flow in Hydrologic Modeling. NATO ASI Series, Vol. 275. Springer, Dordrecht. https://doi.org/10.1007/978-94-009-2352-2_10

Rawls, W. J., Nemes, A., Pachepsky & Ya. (2004). Effect of soil organic carbon on soil hydraulic properties. Development in Soil Science, 30(2004), 95–114. https://doi.org/10.1016/S0166-2481(04)30006-1

Saxton, K. E. & Rawls, W. J. (2006). Soil Water Characteristic Estimates by Texture and Organic Matter for Hydrologic Solutions. Soil Science Society of America Journal, 70(5), 1569–1578. https://doi.org/10.2136/sssaj2005.0117

Schaap, M. G. (2004). Graphic user interfaces for pedotransfer functions. Developments in Soil Science, 30(2004), 349–356. https://doi.org/10.1016/S0166-2481(04)30019-X

Skaggs, T. H. (n.d.). Rosetta soil. GitHub. Retrieved January 2024 from https://github.com/usda-ars-ussl/rosetta-soil?tab=readme-ov-file

Soriano, A. (1992). Río de la Plata grasslands. In R. T. Coupland (Ed.), Natural grasslands: introduction and western hemisphere (pp. 367–407). Elsevier. https://cir.nii.ac.jp/crid/1570854175783394048

Sun, J., Wang, G., Sun, X., Sun, S., Guo, L., Hu, Z., Song, C. & Lin, S. (2024). Soil water dynamics and plant water uptake: Primeval mature vs. debris flow-developed half-mature subalpine fir stands in the eastern Tibetan Plateau. Science of the Total Environment, 951(2024), 175437. https://doi.org/10.1016/J.SCITOTENV.2024.175437

Taylor, K. E. (2001). Summarizing multiple aspects of model performance in a single diagram. Journal of Geophysical Research: Atmospheres, 106(D7), 7183–7192. https://doi.org/10.1029/2000JD900719

Teruggi, M. E. (1957). The Nature and Origin of Argentine Loess. Journal of Sedimentary Research, 27(3), 322–332. https://doi.org/10.1306/74D706DC-2B21-11D7-8648000102C1865D

van Genuchten, M. T. (1980). A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Science Society of America Journal, 44(5), 892–898. https://doi.org/10.2136/sssaj1980.03615995004400050002x

Varni, M. R. & Usunoff, E. J. (1999). Simulation of regional-scale groundwater flow in the Azul River basin, Buenos Aires Province, Argentina. Hydrogeology Journal, 7, 180–187. https://doi.org/10.1007/s100400050190

Vereecken, H., Maes, J. & Feyen, J. (1990). Estimating unsaturated hydraulic conductivity from easily measured soil properties. Soil Science, 149(1), 1–12. https://doi.org/10.1097/00010694-199001000-00001

Weinzettel, P. (2005). Hidrodinámica de la zona no saturada en suelos argiudoles de la cuenca del arroyo Azul. [Tesis de doctorado no publicada]. Universidad Nacional del Sur.

Wösten, J. H. M., Lilly, A., Nemes, A. & Le Bas, C. (1999). Development and use of a database of hydraulic properties of European soils. Geoderma, 90(3–4), 169–185. https://doi.org/10.1016/S0016-7061(98)00132-3

Wösten, J. H. M., Pachepsky, Ya. A. & Rawls, W. J. (2001). Pedotransfer functions: Bridging the gap between available basic soil data and missing soil hydraulic characteristics. Journal of Hydrology, 251(3–4), 123–150. https://doi.org/10.1016/S0022-1694(01)00464-4

Zárate, M. A. (2003). Loess of southern South America. Quaternary Science Reviews, 22(18–19), 1987–2006. https://doi.org/10.1016/S0277-3791(03)00165-3

Zárate, M. A., Tripaldi, A. (2012). The aeolian system of central Argentina. Aeolian Research, 3(4), 401–417. https://doi.org/10.1016/j.aeolia.2011.08.002

Zimmermann, E. D. & Basile, P. A. (2007, May 15). Funciones hidráulicas de suelos limosos: regresiones no lineales con propiedades físicas y granulométricas. XXIº Congreso Nacional del Agua, San Miguel de Tucumán, Argentina. https://www.fceia.unr.edu.ar/curiham/es/wp-content/uploads/2018/11/con10-CNA071.pdf

Zimmermann, E. D. & Basile, P. A. (2008). Uso de funciones de pedotransferencia para la estimación de parámetros hidráulicos en suelos limosos (Llanura Argentina). Boletín geológico y minero, 119(1), 71–80. https://web.igme.es/boletin/2008/119_1_2008/ARTICULO%206.pdf

Zimmermann, E. D. & Basile, P. A. (2011). Estimación de parámetros hidráulicos en suelos limosos mediante diferentes funciones de pedotransferencia. Tecnología y ciencias del agua, 2(1), 99-116. https://www.scielo.org.mx/scielo.php?pid=S2007-24222011000100007&script=sci_arttext

Type of Publication: ARTICLE.

Work received on 26/12/2024, approved for publication on 03/02/2025 and published on 28/02/2025.

HOW TO CITE

Golin, A. S., Mujica, C. R & Villanueva, I. (2025). Soil hydraulic properties database of the Pampas Region in Buenos Aires Province. Cuadernos del CURIHAM, Edición Especial (2024): 40 Años del IHLLA. e09. https://doi.org/10.35305/curiham.ed24.e09