MODELACIÓN HIDRODINÁMICA EN EL TRAMO KM 232-480 DEL RÍO PARANÁ DURANTE LA BAJANTE 2020 A 2022

HYDRODYNAMIC MODELING IN THE KM 232-480 REACH OF THE PARANÁ RIVER DURING THE 2020 TO 2022 LOW WATER FLOW

Gerardo A. Riccardi^(1)(2)(*) y Pedro A. Basile^(1)(**)

⁽¹⁾Departamento de Hidráulica y Centro de Investigaciones Rosario de Investigaciones Hidroambientales, Facultad de Ciencias Exactas, Ingeniería y Agrimensura. Universidad Nacional de Rosario, Argentina.

⁽²⁾Consejo de Investigaciones de la Universidad Nacional de Rosario. Argentina.

^(*)e-mail:riccardi@fceia.unr.edu.ar. ORCID: https://orcid.org/0000-0002-9294-3166

^(**)e-mail: pbasile@fceia.unr.edu.ar. ORCID: https://orcid.org/0000-0001-8826-0621

RESUMEN

Se presenta la simulación hidrodinámica en un tramo del cauce principal del río Paraná entre los km 232 y km 480 en un período que comprende la reciente bajante desde el 01/01/2020 al 31/12/2022, mediante un modelo de complejidad reducida cuasi-2D. El modelo utilizado permitió describir nivel, caudal y velocidad media integrada en la vertical en el dominio espacial discretizado en celdas de 100 m x 100 m. En el tramo existe una importante infraestructura portuaria por lo que resulta de interés la simulación hidrodinámica para aportar a la planificación de las actividades antrópicas y a la evaluación hidroambiental del aprovechamiento, control y gestión del recurso hídrico. En el período de estudio se observaron caudales entre 6800 m³/s y 16000 m³/s correspondiendo al trienio de menor volumen escurrido en lo que va de la serie moderna de niveles desde el año 1971 a la fecha. La señal de entrada consistió en la serie de caudales medios diarios en el borde aguas arriba. Para evaluar la calidad de la simulación se compararon niveles diarios observados y calculados en los hidrómetros en 6 sitios: Puerto San Martín (km 448), Rosario (km 416), Villa Constitución (km 368), San Nicolás (km 353), Ramallo (km 325) y San Pedro (km 276). Asimismo, se evaluaron valores máximos, mínimos y medios de niveles y amplitud del rango de variación de niveles. Además, se compararon las permanencias de niveles y relaciones niveles-caudales en los sitios. En la integralidad del ajuste logrado, los resultados pueden calificarse como muy buenos.

Palabras clave: hidrodinámica, río Paraná, bajante, modelación cuasi2D, modelo de complejidad reducida.

ABSTRACT

The hydrodynamic simulation of the Parana River in the reach km 232-480 during the low flows years 2020-2022 is presented. The simulations were carried out by using a reduced complexity quasi-2D hydrodynamic model, appropriated to represent the evolution of water level, discharge and depth integrated mean flow velocity in the modeled domain discretized with 100 m x 100 m grid cells. In the modeled river reach there is an important port infrastructure, so hydrodynamic simulations are of interest to contribute to the planning of anthropogenic activities and the hydro-environmental evaluation of the use, control and management of water resources. During the period of time simulated in this study, discharges between 6800 m³/s and 16000 m³/s were observed, corresponding to the three-year period with the lowest drained volume registered in the modern series of water levels from 1971 to date. The series of mean daily discharges were assigned as the upstream boundary condition. In order to evaluate the quality of the simulation, daily water levels observed and calculated in the hydrometers at 6 sites were compared: Puerto San Martín (km 448), Rosario (km 416), Villa Constitución (km 368), San Nicolás (km 353), Ramallo (km 325) y San Pedro (km 276). Moreover, maximum, minimum and average values of water levels and amplitude of the range of variation were evaluated. In addition, the duration of water levels and stage-flow relationships in the 6 sites were compared. In the comprehensiveness of the adjustment achieved, the results can be described as very good.

Keywords: hydrodynamics, Paraná river, low flows, quasi-2D modeling, reduced complexity.

INTRODUCCIÓN

El tramo en estudio comprende una longitud del río de 248 km aproximadamente, cuyo cauce principal presenta múltiples bifurcaciones y confluencias, conformando una red de cauces de diversas jerarquías e islotes centrales. El tramo se ubica al oeste del humedal o planicie de inundación del río, la cual es sometida a ciclos de crecidas y bajantes de acuerdo a los hidrogramas entrantes desde el tramo Paraná medio, como así también, a perturbaciones de niveles (especialmente en la zona aguas abajo) debido al ciclo periódico de las mareas en el océano y a sudestadas que también se presentan en la desembocadura en el río de la Plata. En el tramo se emplazan sobre la margen derecha diversas ciudades de distintas magnitudes como Puerto San Martín, San Lorenzo, Fray Luis Beltrán, Capitán Bermúdez, Granadero Baigorria, Rosario, Villa Gobernador Gálvez, Arroyo Seco, Villa Constitución, San Nicolas, Ramallo y San Pedro por lo cual, se sitúan también diversas obras de toma de agua, descargas de efluentes pluviales, cloacales e industriales que pueden verse perturbadas en su funcionamiento en función de los niveles del río. Las variaciones de los niveles también pueden condicionar las actividades laborales y recreativas de los diferentes actores del territorio costero. En el mismo sentido un importante número de instalaciones portuarias (puertos de carga, comerciales y náuticos) se ubican en el tramo pudiendo ser afectados su funcionamiento en períodos críticos tanto de bajantes como de crecientes. Además, sobre el cauce principal se desarrolla la vía de navegación troncal (VNT) Santa Fe- Océano. En la misma se sitúan 14 pasos críticos donde regularmente se hacen trabajos de dragado para garantizar profundidades efectivas compatibles con las de diseño. Resulta evidente que en estos casos una certera determinación de los niveles de agua resulta de importancia para la realización de las operaciones de dragado de mantenimiento y el cómputo de los volúmenes de sedimentos involucrados.

En este marco, se plantea el desafío de describir la hidrodinámica del sistema con la mayor confiabilidad técnica compatible con una herramienta de simulación de baja complejidad en el contexto de la bajante severa del río Paraná entre 2020 y 2022. Las características del tramo modelado en su extensión territorial, la disponibilidad de datos y la factibilidad de llevar adelante una modelación computacionalmente ventajosa hace que sea factible emplear modelos de complejidad reducida (Nicholas et al., 2012) los que, con ecuaciones más simplificadas que los modelos completos y a un costo computacional menor, permiten describir las variables principales del flujo con un aceptable nivel de aproximación en dominios espacio/temporales de extensas zonas de inundación y a largo plazo (Wilson et al., 2009). Hasta el momento se ha avanzado en la modelación hidrodinámica del curso principal experimentando con una grilla de cálculo del tipo cuadrangular con 100 m de lado. Se busca con esta discretización establecer una escala de representación de la bidimensionalidad del flujo en el cauce principal en un extenso tramo, compatible para la futura incorporación de la planicie de inundación con similar nivel de detalle.

En un sub-tramo del orden de 50 km han sido implementados modelos hidrodinámicos 2DH completos, tanto en condiciones de flujo permanente considerando un amplio rango de caudales desde aguas bajas a altas; como así también, en flujo impermanente (Basile et al., 2016; Peruzzo et al., 2017). Por su parte el trabajo de Garcia et al. (2015, 2017) comprendió la modelación hidrodinámica e hidrosedimentológica y estudio de aforos en el cauce principal y el valle de inundación en un tramo desde la zona desde Diamante a Ramallo, con un dominio de celdas irregulares. La modelación fue realizada con el CTSS8 (Riccardi, 2000) y FLUSED (Basile et al., 2007).

En el tramo completo simulado en el presente estudio, han sido realizadas modelaciones antecedentes donde se ha verificado el funcionamiento del modelo de complejidad reducida cuasi-2D en régimen impermanente en crecientes, con un rango de caudales variando entre 15900 m³/s ≤ Q ≤ 26400 m³/s, verificándose una calificación global del ajuste en términos de niveles diarios entre buena y muy buena (Peruzzo et al., 2016). Otros avances de modelaciones parciales durante el transcurso de la bajante se presentaron en Riccardi et al. (2022) y Riccardi y Basile (2023).

Otros trabajos de simulación en un tramo que involucró gran parte de los ríos y canales del delta del río Paraná fueron realizados por Sabarots Gerbec (2014) quien aplicó un modelo matemático hidrodinámico unidimensional en la red de ríos y canales del río Paraná en la región del Delta Superior (Diamante a Villa Constitución) y Delta Medio (Villa Constitución a Puerto Ibicuy). El software utilizado fue el conocido HEC-RAS. La serie temporal modelada comprendió desde 2010 a 2013 con una discretización media de 10 km. En el período los niveles del río se pueden caracterizar como estados de aguas medias y medias altas. El autor concluye que, si bien los errores en la simulación no son menores, el traslado de la onda de crecida fue bien representado por indicadores de bondad de ajuste, como el coeficiente de Nash-Sutcliffe con valores próximos a la unidad.

Re et al. (2015) presentan la descripción espacial del comportamiento de los niveles en el Delta del río Paraná incorporando el Delta Inferior (Ibicuy a río de la Plata) a partir de los resultados de una modelación hidrodinámica unidimensional en un período temporal de 1994 a 2013. La discretización espacial fue de 5 km. El modelo hidrodinámico se basó en el propuesto por Sabarots Gerbec (2014) que incluyo Delta Superior y Medio y la representación del Delta Inferior de Bombardelli et al. (1994). Los autores concluyen que el modelo permitió realizar análisis conceptuales sobre el comportamiento de la red de canales y la comprensión del comportamiento de distintos brazos durante crecidas y la relación de caudales en las bifurcaciones, y las implicancias de la onda de marea en el Bajo Delta. Re et al. (2015) destacan como el principal resultado de su trabajo a la caracterización estadística de niveles en cualquier sitio del delta del río Paraná a partir de series obtenidas con simulaciones.

En el trabajo de Sabarots Gerbec y Borus (2016) se lleva a cabo la caracterización hidrodinámica en aguas bajas para la VNT partiendo del modelo numérico validado por Sabarots Gerbec (2014). El modelo fue validado tanto para niveles y caudales, y a partir de la simulación desde 1975 a 2016 se obtuvieron resultados de niveles y caudales para los principales puertos de la VNT entre Santa Fe y el río de la Plata, considerándose como confiables los resultados para estaciones aguas arriba de Baradero. A partir de los resultados, los autores concluyen que los mismos constituyen un punto de referencia útil para el diseño y operación de terminales portuarias.

Sabarots Gerbec et al. (2018) presenta simulaciones realizadas con una actualización geométrica del modelo precedente presentado por Re et al. (2015), obteniendo resultados en lo que respecta a la repartición de caudales en diferentes bifurcaciones en la red de canales que componen el Delta del río Paraná. Fue simulada una serie desde 1997 a 2013. Las particiones obtenidas se describieron en función dos variables: (i) el caudal ingresante a la bifurcación y (ii) el nivel de superficie libre en la desembocadura en el río de la Plata. Los autores concluyen que cuando hay grandes caudales en el río Paraná y niveles bajos de restitución en el río de la Plata implican dispersiones bajas en los rangos de partición. En el caso de bajos caudales y altos niveles de restitución el rango determinado en la partición es mucho más disperso con casos de presentación de flujo inverso.

Morale et al. (2020) presentan la aplicación de un modelo hidrodinámico bidimensional para su utilización en el marco de un esquema de toma de decisiones para el desarrollo espacial sustentable en el territorio del Delta del río Paraná. El modelo se empleó para evaluar los impactos de diferentes intervenciones antrópicas en el delta. El área de trabajo comprendió desde la zona deltaica de Villa Constitución hasta Campana y Canal Nuevo.

Guizzardi et al. (2022) desarrollaron la implementación de un sistema de pronósticos de niveles de aguas en diferentes sitios del delta del río Paraná. El sistema se compone de una estructura integrada de modelización y predicción, teniendo en cuenta las interacciones del escurrimiento, las tormentas, oleaje y las mareas. La estructura está compuesta por un modelo hidrodinámico unidimensional aplicado en la red de ríos y canales componentes del delta del río Paraná desde Paraná (aguas arriba) hasta el río de la Plata, un modelo bidimensional del estuario del Río de la Plata, dos modelos de predicción numérica del tiempo y esquemas de modelos autorregresivos para corregir los pronósticos con datos observados. El modelo unidimensional implementado es una actualización de los trabajos de Re et al. (2015). Originalmente el modelo estuvo basado en la propuesta de Sabarots Gerbec (2014), que incluye el Delta Superior y el Delta Medio. Según documenta Guizzardi et al. (2022), la incorporación del Bajo Delta fue tomada de la representación de Bombardelli et al. (1994). Además, el modelo fue utilizado anteriormente para generar estadísticas de niveles en el Delta del río Paraná (Re et al., 2015) y para la caracterización de niveles mínimos en la hidrovía (Borús y Sabarots Gerbec, 2015). Este modelo resuelve la hidrodinámica unidimensional de la compleja red de cursos de agua desde Paraná hasta el río de la Plata. Los modelos del estuario del río de la Plata proveen las condiciones de borde para el modelo unidimensional de la red de ríos y canales. La estructura integrada fue denominada HIDRO-DELTA, concluyendo que la performance del sistema es satisfactoria como herramienta de pronóstico de niveles de agua.

OBJETIVOS

El objetivo principal del trabajo fue evaluar al modelo matemático cuasi-2D de baja complejidad CTSS8RIO en sus capacidades de reproducción de la hidrodinámica de la bajante extrema en el cauce principal de río Paraná Inferior en vista a su utilización como herramienta de pronóstico de niveles en escenarios donde se imponga como señal de entrada una serie de caudales medios diarios ingresantes al tramo y en el borde aguas abajo una relación altura-caudal.

METODOLOGÍA

En la primera etapa de la modelación se impusieron condiciones de borde del tipo altura-tiempo, tanto en el borde aguas arriba como en el borde aguas abajo y se realizaron simulaciones variando el coeficiente de rugosidad de Manning. Para cada proposición de rugosidades, se determinaron los niveles de agua en cada una de las celdas del dominio espacial. En los 6 sitios de los hidrómetros se compararon los niveles simulados con los niveles observados provistos por la Dirección Nacional de Vías Navegables Delegación Paraná Inferior (DNVN-DPI) (2023). Además, se determinó el hidrograma entrante, que fue comparado con los caudales aforados por el Sistema Nacional de Información Hidrológica (SNIH) (2023) y también con los caudales medios diarios estimados por SNIH (2023) y los caudales estimados en Basile y Riccardi (2023).

La segunda etapa de la modelación consistió en la evaluación del modelo como herramienta de predicción. En el borde aguas abajo se definió una relación H-Q, de modo que, considerando como señal de entrada en el borde aguas arriba el hidrograma determinado en la primera etapa, se simularon los niveles con la mayor aproximación posible a los niveles observados en los hidrómetros. Esta potencialidad del modelo permite su utilización como predictor en cualquier evento real o hipotético de caudales que se requiera analizar. Para establecer la bondad de los resultados se compararon las series de niveles hidrométricos calculados y observados, como así también, las curvas de permanencias de los niveles hidrométricos y de las profundidades efectivas en la VNT a lo largo del trienio.

MATERIALES Y METODOS

El modelo de simulación hidrodinámica

El modelo de simulación empleado es el CTSS8RIO, que se trata de una versión adaptada del CTSS8 (Riccardi, 2000) conjuntamente con la plataforma de pre y post-procesamiento SIMULACIONES 2.0 (Stenta et al., 2005), siendo de tipo cuasi-2D difusivo, no contemplando efectos inerciales ni de cierre de turbulencia. El planteo de las ecuaciones para resolver el tránsito hidrodinámico en forma simplificada en dos dimensiones es (Figura 1):

Ecuación de continuidad:

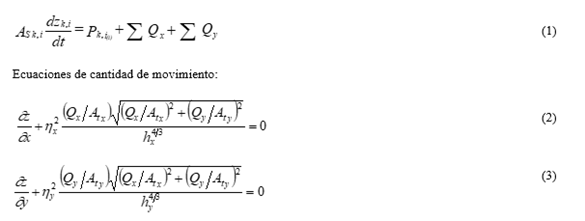
Donde z_k,i es el nivel del agua en la celda i; A_sk,i es el área superficial mojada en la celda i; P_k,i es el ingreso/egreso de caudales externos; Q_x y Q_y , ƞ_x y ƞ_y, h_x y h_y , A_{t x} y A_{t y} son los caudales intercambiados, los coeficientes de rugosidad de Manning, las profundidades de flujo y las áreas transversales consideradas entre las celdas vinculadas en el sentido x e y respectivamente.

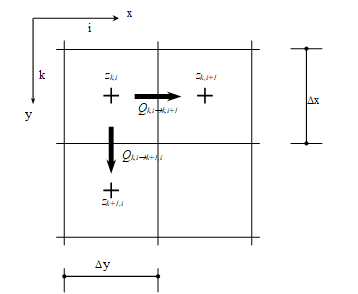
Figura 1. Definición de variables de flujo en la grilla.

El tramo en estudio

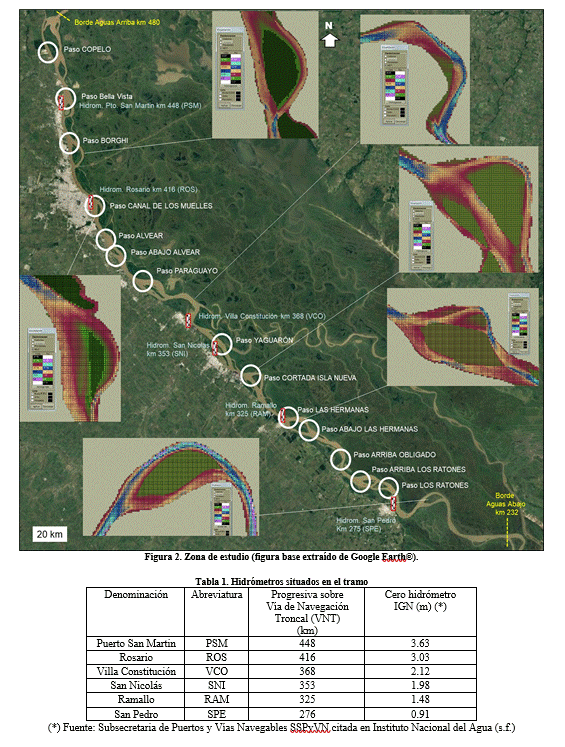
El tramo modelado tiene una extensión de 248 km, abarcando 502 km² del cauce principal del río Paraná, cauces secundarios e islas centrales (Figura 2). Se extiende desde el km 232 cercano a la denominada “bifurcación” donde se bifurca en el Paraná de las Palmas y el Paraná Guazú, hasta el km 480 sitio aguas arriba de Puerto San Martín y aguas abajo de Diamante. El ancho del curso principal es altamente variable con valores desde 700 m hasta 2200 m. En zonas donde se conformaron islas centrales el ancho total llega en algunos sitios a 4600 m. A macro-escala, el cauce principal muestra una configuración morfológica caracterizada por una sucesión de expansiones, donde se observan islas vegetadas, interconectadas con tramos más estrechos y profundos (Basile et al., 2015). El lecho es de arena con d₅₀ variando entre 0.26 mm y 0.32 mm (Basile y Riccardi, 2002).

En el tramo se emplazan 6 hidrómetros en los cuales se miden niveles diarios y en el caso de Prefectura Naval Argentina, 2 niveles diarios. Los lugares y ceros considerados en este estudio de los hidrómetros se sintetizan en la siguiente Tabla 1. La información de relevamientos batimétricos como de niveles de agua aforados en los diferentes hidrómetros fueron convertidos en cotas con referencia IGN mediante los ceros indicados en Tabla 1.

A lo largo del tramo se emplazan en su margen derecha múltiples obras de toma de agua y obras de volcamiento de efluentes pluviales, cloacales e industriales, instalaciones portuarias, como así también, se desarrolla parte de la VNT Océano-Confluencia, obras cuyos funcionamientos e impactos producidos pueden verse fuertemente modificados por los bajos niveles del río. En la VNT se sitúan 14 pasos críticos donde regularmente se hacen trabajos de dragado para garantizar profundidades efectivas compatibles con las de diseño. La profundidad de diseño actual de la VNT es de 10.97 m (36 pies) hasta el km 460 y de 8.23 m (27 pies) desde km 460 hacia aguas arriba, vinculándose a los denominados niveles de referencia (NR) que se definen en cada sitio de localización de los hidrómetros. Cada NR corresponde a un nivel que es igualado o superado un 80% del tiempo (permanencia), y se establece a partir series históricas de niveles. El brazo principal donde se desarrolla la VNT tiene anchos variables entre 400 m y 2800 m y profundidades que pueden variar entre los 45 m y 10 m. La VNT tiene una traza (variable) que involucra las zonas más profundas, con un ancho en su mayor parte de 116 m.

El modelo digital del fondo del cauce

El modelo digital con que se representó el cauce del río e islas interiores fue construido a partir de las siguientes fuentes de información:

(i) Cauce principal río Paraná. Relevamiento Batimétrico (DNVN-DPI, 2014)

(ii) Cartas Náuticas. Servicio de Hidrografía Naval (SHN) (2018) (Figura 3)

(iii) Relevamientos Batimétricos Canal de Navegación. Subsecretaría de Puertos, Vías Navegables y Marina Mercante (SSPVNyMM) (2020)

(iv) Estudios Complementarios Hidráulicos y Morfológicos de la Zona de la Isla de la Invernada. Facultad de Ingeniería y Ciencias Hídricas (FICH) (2006).

Los relevamientos de fondo del cauce disponibles y provistos por DNVN-DPI (2014) estaban sectorizados cada 10 km, medidos sobre el eje de la VNT y referenciados a un cero interpolado entre los 2 hidrómetros más cercanos. Por lo cual hubo que vincular al 0 del IGN cada tramo y luego realizar la integración completa del tramo a modelar. Los perfiles transversales disponibles se ubicaron cada 100 m (en la dirección de flujo) y los puntos en la dirección transversal cada 20 m. En el canal de navegación la morfología del fondo fue mejorada a partir de los relevamientos descargados de la página de la SSPVNyMM (2020), donde se contó con cotas del fondo cada 10 m en el sentido del flujo y sobre 3 alineaciones longitudinales en el eje de la VNT y sobre los veriles derecho e izquierdo. En la zona de islas la cota de terreno fue extractada a partir del modelo digital del terreno (MDT) disponible en Google Earth©. Con la información de cota de fondo en cauce principal e islas referidas al IGN, se construyó un modelo digital de elevación (MDE) del fondo en una grilla cuadrangular de 100 m x 100 m mediante el método de krigging, utilizando el software Surfer 9.0©. En la Figura 4 se presenta el MDT empleado en la modelación.

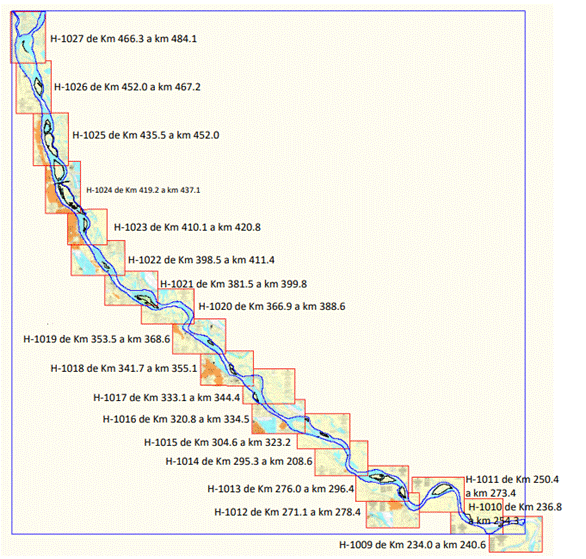
Figura 3. Cartas Náuticas comprendidas en el tramo de modelación.

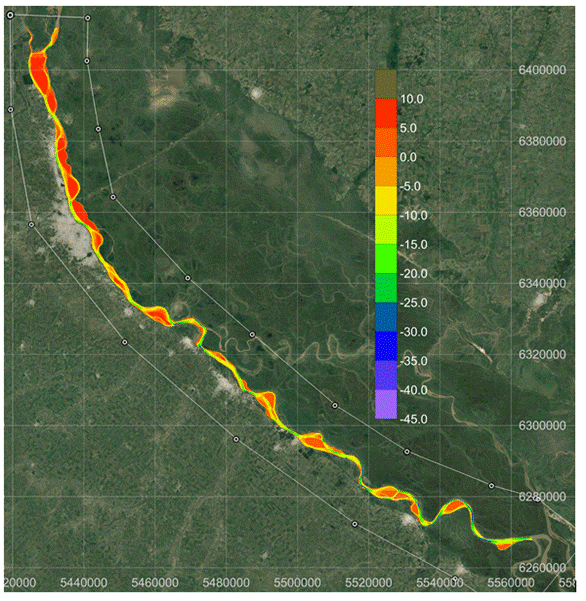
Figura 4. Modelo digital del fondo rasterizado en celdas de 100 m x 100 m. Cotas de fondo en (m), referidas a IGN. Georreferenciación en Sistema de Proyección Gauss-Kruger Faja 5.

Sobre la representación del fondo del cauce

Tal como mencionado anteriormente, la información de cotas del fondo estuvo mayormente extraída a partir de perfiles transversales (con trayectoria en sentido perpendicular a la corriente principal) cada 100 m y en cada perfil transversal puntos cada 20.0 m. Por lo tanto, ni en el relevamiento ni en el MDT del fondo construido, se representa en detalle las formas de fondo con dimensiones menores a 100 m en el sentido de la corriente. A modo de ejemplo ilustrativo se presenta en Figura 5(a) un perfil longitudinal relevado en el año 2016 en el eje del canal de navegación por el Organismo de Control de la VNT Santa Fé-Océano con la discretización original de 1 punto cada 10 m y una discretización agregada a 1 punto cada 100 m a los efectos de su uso en la modelación. En la Figura 5(b) se presenta un detalle ejemplificativo en el tramo km 355-357. Claramente, puede inferirse que la representación del fondo por parte del relevamiento base debe considerarse como una aproximación al valor medio del fondo y por lo tanto el modelo no podrá representar la rugosidad por formas de fondo por lo que esta característica se deberá representar como un agregado “ficticio” a la rugosidad de superficie.

Asimismo, vale destacar que las dunas se desplazan con movimiento ondulatorio con una celeridad, diferenciada a la del flujo, hacia aguas abajo modificando amplitudes y longitudes. La amplitud y la longitud de estas formaciones está directamente vinculada (entre otras cosas) con la profundidad de flujo. En este contexto, cuando se modela este tipo de cauces fluviales lo que se representa es una conformación “media del fondo”, donde se asume que la forma de fondo que se incorpora al modelado es el valor medio de los puntos altos (cresta) y puntos bajos (valle) de las diferentes dunas que circulan por el fondo. En la Figura 5(c) se presenta la banda de oscilación de la cota de fondo al superponer perfiles longitudinales de 2010 a 2015 en un tramo de 10 km, dicha banda en el subtramo entre km 419 a 429 desarrolla una dimensión en altura entre 4 a 5 m.

En lo que respecta a la representación de los perfiles transversales la agregación de la información trae como consecuencia que el perfil real se aproxime a un perfil escalonado con discretización de 100 m. A modo de ejemplo se presentan las siguientes Figuras 6(a) a 6(d), donde se puede visualizar la aproximación introducida en 4 secciones cualquiera del dominio espacial de modelación. Además, en la Figura 6(e) se representa la variación de cotas de fondo por los movimientos de las formaciones de fondo en la sección transversal del km 421.6 entre los años 2009 a 2018.

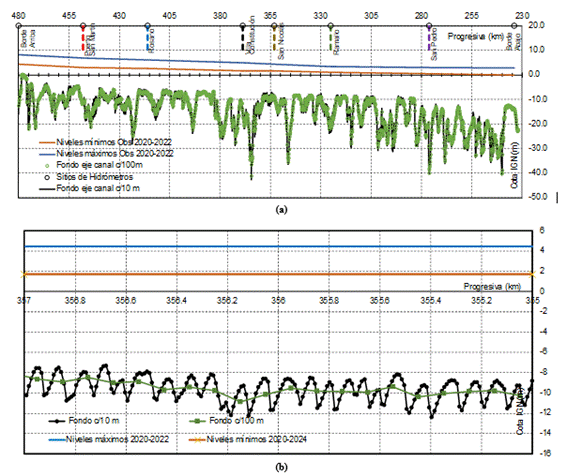
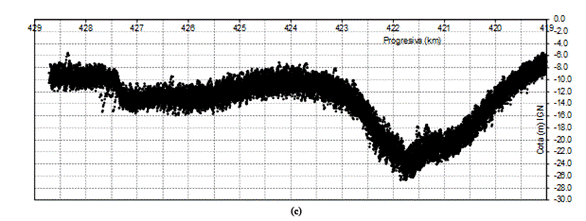
Figura 5. Perfiles longitudinales del fondo en el eje de la VNT; (a) Relevamiento discretizado c/10 m e interpolado c/100 m (relevamiento año 2016); (b) Detalle de representación en tramo km 355 a 357 c/10 m y c/100 m (relevamiento año 2016);

(c) Entorno de oscilación de formaciones de fondo en tramo km 419 a 429 (relevamientos de años 2009 a 2018).

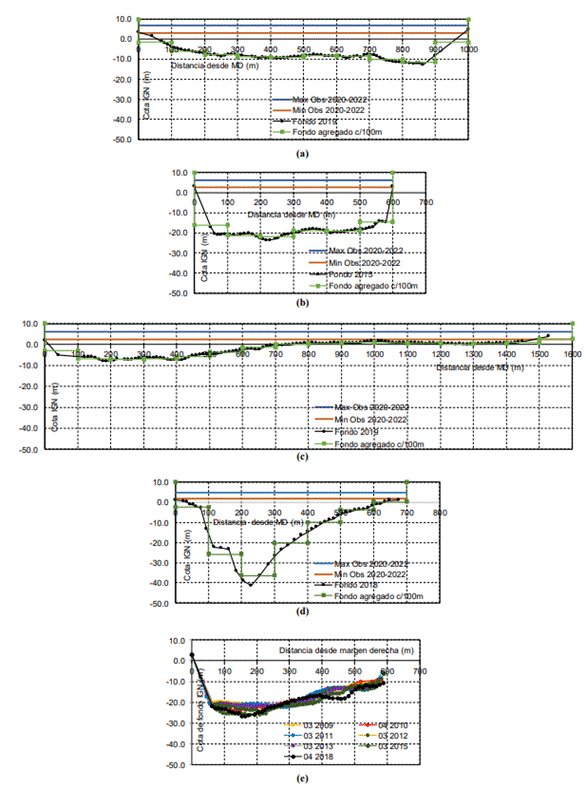
Figura 6. Perfiles transversales relevados y modelados: (a) km 448; (b) km 421; (c) km 416; (d) km 364; (e) Variación del fondo por movimiento de formaciones de fondo km 421.6 de 2009 a 2018.

Pasos críticos para la navegación en la VNT

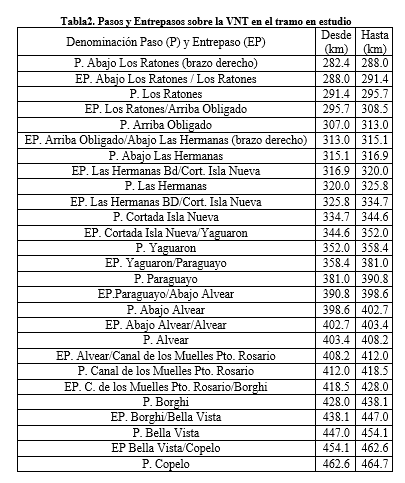
Sobre la VNT se sitúan 14 pasos críticos y entrepasos (EP) donde regularmente se hacen trabajos de dragado (y volcamiento) para garantizar profundidades efectivas compatibles con las de diseño. Durante la bajante se presentaron una determinada cantidad de días donde no se garantizaron las profundidades de proyecto por lo cual existieron restricciones al calado de los buques que navegaron por la VNT. En la Figura 2 se presentan las ubicaciones de los pasos críticos en tanto que en la Tabla 2 se presentan las denominaciones de los pasos y entrepasos y las progresivas aproximadas de sus ubicaciones a la VNT. Precisamente tanto en la etapa de calibración como de explotación del modelo una de las comparaciones para evaluar la performance del modelo fue comparar las curvas de permanencias observadas y calculadas de niveles hidrométricos.

Constitución del modelo

De acuerdo con la discretización espacial escogida para el modelado (celdas cuadradas de 100 m x 100 m), se emplearon 50244 celdas y 97129 vinculaciones. De total de celdas aproximadamente un 40% corresponden a la representación de islas centrales y zonas márgenes del curso, en tanto que un 60% corresponde al cauce principal y cauces secundarios.

La información necesaria de cada celda es su cota de fondo y la necesaria en cada vinculación es la rugosidad.

Las condiciones de borde fijadas en el modelo durante la calibración fueron (i) nivel en función del tiempo H(t), en celdas del borde entrante y (ii) nivel en función del tiempo, H(t) en celdas del borde saliente. Es necesario destacar que se consideraron dos bordes salientes. El borde saliente principal se ubicó en el extremo aguas abajo del modelo (km 232) donde escurre aproximadamente un 95% del caudal entrante, en tanto que se fijo también un borde saliente coincidente con la derivación de río Pavón a la altura del km 368 en las proximidades del hidrómetro de Villa Constitución.

Las condiciones de borde fijadas en la segunda etapa consistieron en (i) borde entrante ídem a la primera etapa y (ii) borde saliente se propusieron condiciones del tipo nivel-caudal Q(H). Como se mencionó, la operación del modelo imponiendo la condición de borde H(Q) permitió evaluar la performance del modelo para emplearse en simulaciones de escenarios hipotéticos donde no se conocen previamente las relaciones H(t) en ningún punto interno ni en los bordes entrantes y salientes.

Calibración del modelo

Al tratarse de un modelo de baja complejidad, el único parámetro de calibración con que cuenta es el coeficiente de rugosidad en las 2 direcciones ortogonales fijadas al constituir el modelo. En la definición de las ecuaciones del modelo, la velocidad es vinculada a la profundidad de agua mediante la ecuación de Manning por lo que el coeficiente de rugosidad de Manning se convierte en el parámetro que representa la resistencia al escurrimiento pero así también engloba, en forma aproximada, otros mecanismo de resistencia al escurrimiento que no son descriptos por las ecuaciones gobernantes (1), (2) y (3).

El proceso de calibración comprendió una serie de simulaciones considerando rugosidad uniforme en todo el tramo y variando el coeficiente de rugosidad en el rango 0.027 s/m^1/3 ≤ ƞ ≤ 0.032 s/m^1/3. Las simulaciones se realizaron en el trienio del 01/01/2020 al 31/12/2022.

Cabe destacar que al proponer la modelación para calibración con señal de entrada H(t) en el borde entrante y H(t) en el borde saliente, el modelo genera internamente en función de su constitución y fundamentalmente de la rugosidad propuesta, el caudal intercambiado y velocidad entre cada celda constitutiva como así también el volumen de agua almacenado para cualquier tiempo de la modelación. En función de esto, la bondad de la calibración fue evaluada a partir del mejor ajuste en términos de niveles diarios en cada uno de los 6 hidrómetros y la comparación del hidrograma generado en el borde entrante y su comparación con los estimados por la SNIH (2023) y los aforados por SNIH (2023).

Tras las corridas de calibración se comprueba que con los coeficientes de rugosidad variando en el rango indicado anteriormente, los ajustes a los limnigramas observados en los 6 hidrómetros son calificados como muy buenos. Por otro lado, los caudales generados en la modelación constituyen una banda en la cual quedan agrupados el 97% de los caudales diarios estimados por SNIH (2023), los aforados por SNIH (2023) en la estación Timbues (próxima a PSM) y los estimados por Basile y Riccardi (2023). Tras esta valoración del ajuste se asumió como mejor ajuste el que se logra con un coeficiente de rugosidad ƞ = 0.0295 s/m^1/3 y considerando un márgen de error ± 0.0025 (± 9.0%). En la Figura 7 se presentan el hidrograma generado con el mejor ajuste considerado, los valores de caudales medios diarios (serie discontinuada) estimados por SNIH (2023) y los caudales aforados en PSM por SNIH (2023), además en la curva de caudales generados se han agregado las barras de error determinadas en un ± 9.0%.

En la Figura 8 se presentan los limigramas observados y simulados asociados a cada uno de lo 6 sitios de hidrómetros del tramo. En Tabla 3 se presentan un resumen de los errores evaluados en cada limnigrama al comparar valores de niveles diarios simulados con observados. En lo que concierne a errores de valores extremos individuales fueron determinados los errores entre valores máximos y valores mínimos y en lo que concierne a errores globales se determinaron la eficiencia de Nash-Sutcliffe (NS), el coeficiente de correlación (R2) y el error típico (ET).

Al analizar los errores de valores mínimos, el modelo tiende a determinar niveles mínimos inferiores a los observados en tanto que no evidencia una tendencia en lo que tiene que ver con los valores máximos. Asimismo, se evidencia en los hidrómetros aguas abajo de SNI, RAM y SPE errores de extremos mayores en valor absoluto a los de agua arriba. Se hipotetiza que estos errores se deben mayormente a mecanismo del escurrimiento asociados a los ciclos diarios de mareas como así también las ocasionales sudestadas que se manifiestan en el río de la Plata, cuyos movimientos no pueden ser descritos en su totalidad por este modelo de baja compejidad. Si bien en este proceso de calibración los niveles aguas abajo como aguas arriba están ciertamente condicionados o “atados” por las condiciones de borde impuestas de H(t) en cada frontera, se evidencia una multiplicidad de mecanismos hidrodinámicos que no pueden ser representados en su totalidad por el modelo. Cabe agregar que la discretización temporal de la información de borde de 1 día, no permite introducir alteraciones del regimen de niveles subdiarias que pueden introducir tanto las mareas o tormentas y que se propagan hacia aguas arriba.

Por otro lado, la evaluación de bondad del ajuste de las series temporales mediante el ET se acota en 0.17 m, el NS tiene promedio de 0.90 con un mínimo de 0.80 y R2 toma valores emtre 0.93 y 1.00, pudiendose calificar como un ajuste Muy Bueno.

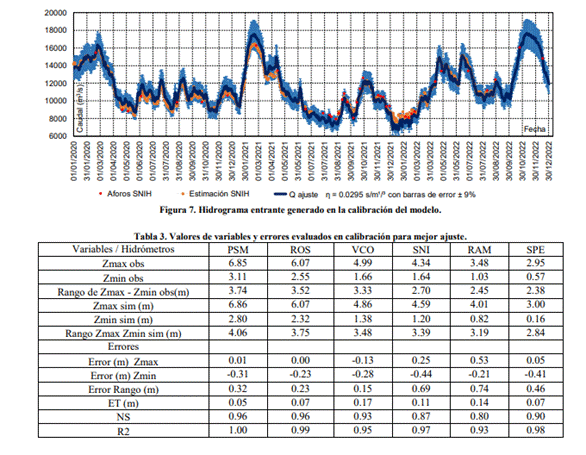
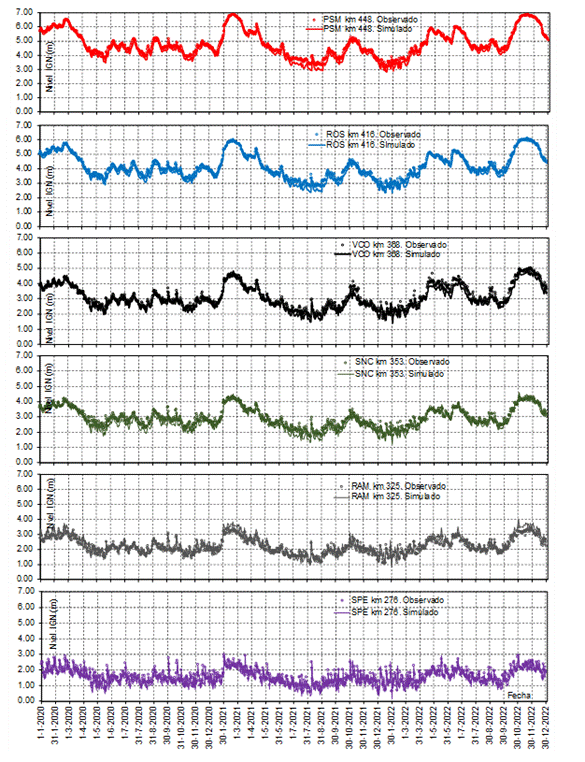
Figura 8. Limnigramas Observados y Simulados en los sitios de los hidrómetros.

EVALUACIÓN DEL MODELO COMO HERRAMIENTA DE PREDICCIÓN

Como fuera mencionado, en esta etapa de la modelación se aplicó el modelo como herramienta de predicción evaluándose su bondad. Se buscó analizar esta capacidad para verificar su aptitud como predictor en cualquier evento real o hipotético de caudales que se requiera analizar. Para lograr que el modelo se comporte como una herramienta de predicción se procedió a cambiar las condiciones de borde planteada en el proceso de calibración. En este sentido, se utilizó como señal en el borde entrante una relación Q(t) y en los bordes aguas abajo se testearon diversas relaciones H-Q.

Para las nuevas condiciones de borde el modelo fue alimentado en el borde aguas arriba con un hidrograma que correspondió al generado en la primera etapa del estudio y en los bordes aguas abajo se trabajó de forma diferenciada. En el borde del río Pavón se asumió que el caudal saliente fue del orden del 5% del caudal entrante y se fijó una relación H-Q a partir de condiciones geométricas e hidráulicas. En cambio, en el borde aguas abajo del km 232, claramente influenciado por los ciclos diarios de mareas y por tormentas en el río de la Plata se forzó la definición de una relación biunívoca H-Q que estableciera la mejor bondad de ajuste en la comparación de los limnigramas calculados y observados en los sitios de los hidrómetros. Además, se compararon las curvas de permanencias de los niveles hidrométricos y de las profundidades efectivas en la VNT a lo largo del trienio.

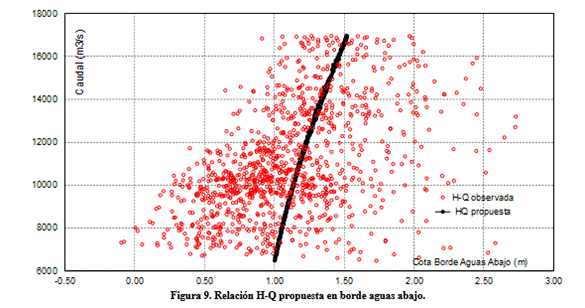
En la Figura 9 se presenta la curva H-Q propuesta en el borde aguas abajo que determinó el mejor ajuste en la prueba de bondad del ajuste. Claramente puede observarse la relación cota-caudal no es biunívoca, lo que condiciona la respuesta de este modelo y cualquier otro de mayor complejidad.

Evaluación de funcionamiento como predictor de niveles en los sitios de los hidrómetros

Para evaluar la bondad de la modelación con el coeficiente de rugosidad uniforme η = 0.0295 s/m^1/3 y con la relación H-Q biunívoca impuesta en el borde abajo se utilizaron los mismos indicadores que en la primera etapa, adicionándose el análisis de la capacidad del modelo para determinar las curvas de permanencias de las profundidades efectivas.

En la Tabla 4 se presenta un resumen de los errores evaluados en cada limnigrama al comparar valores de niveles diarios simulados con observados, los errores entre valores máximos y valores mínimos, la eficiencia de Nash-Sutcliffe (NS), el coeficiente de correlación (R2) y el error típico (ET). En esta configuración del modelo también fueron evaluados los niveles calculados en los bordes aguas arriba (km 480) y aguas abajo (km 232). Se aclara que el nivel en la condición de borde saliente en el río Pavón no se incorpora en la Tabla 4 pues se asume incluída con la evaluación de los niveles en el sitio VCO (km 368). En la Figura 10 se presentan las graficaciones de los limnigramas observados y simulados en las 6 localizaciones de los hidrómetros.

Del análisis global de los errores de valores extremos y de la series integrales se evidencia que excepto en el sitio del hidrómetro SPE (km 276) y en el borde saliente aguas abajo (km 232), la calificación de la aproximación puede considerarse entre Excelente y Muy Buena, incluso se mejoran algunos indicadores respecto a las modelaciones imponiendo relaciones H(t) en ambos bordes, cuando se ajustó el coeficiente de rugosidad. Respecto a la bondad de la aproximación en la zona de SPE, solo alcanza un valor entre Regular-Aceptable y No Aceptable en el borde aguas abajo. Sin dudas el forzado de una condicón H-Q biuníboca tan disímil a la relación observada (Figura 9) se traduce en un rango de cálculo de alturas en las cercanías del borde aguas abajo mucho menor al real observado. Si analizamos la curva H-Q propuesta, el rango de variación de niveles observados para caudales mínimos (~7000 m³/s) está en un rango desde -0.10 m [ Z_{aba obs} [ 2.65 m en tanto que en la zona de caudales máximos (>16000 m³/s) está en un rango entre 0.90 m [ Z_{aba obs} [ 2.40 m, por otro lado la curva H-Q resultante de la mejor aproximación en el tramo, se logró forzando a que tomara valores de Z_{aba sim} = 1.00 m para Q = 6300 m³/s y Z_{aba sim} = 1.50 m para Q = 16700 m³/s.

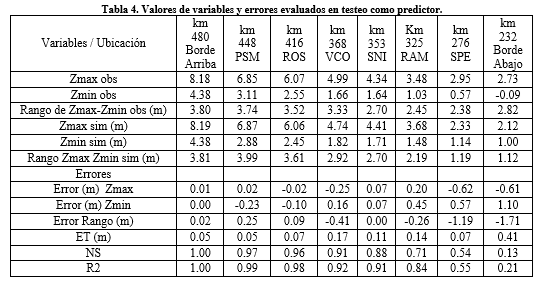
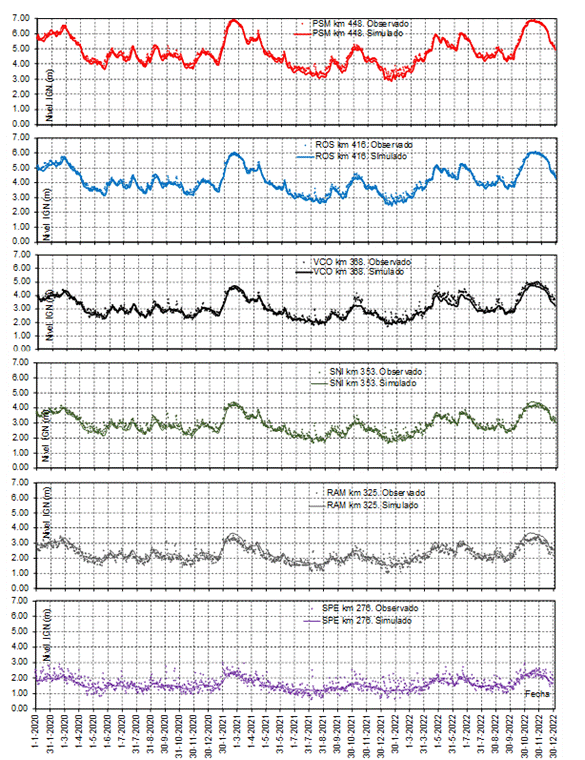
Figura 10. Limnigramas observados y simulados en evaluación del modelo como predictor.

Permanencias de profundidades efectivas en la Vía de Navegación Troncal en el trienio de la bajante

Sin duda que, además de predecir los niveles con un adecuado umbral de exactitud, otra de las capacidades de interés del modelo y de esta modelación en particular, es evaluar la bondad con que permite predecir las permanencias de los niveles en determinados sitios de interés. Una particular importancia de esta capacidad del modelo lo constituye para la planificación de la navegación y posibles operaciones de dragado y mantenimiento en la VNT. En este sentido, a partir de la existencia antecedente de una profundidad de diseño de la VNT de 36 pies (10.97 m) en gran parte del tramo en estudio, se analizó la permanencia de las profundidades efectivas observadas y simuladas en los sitios de los hidrómetros. En la Figura 11 se presentan las representaciones gráficas resultantes del análisis y se adicionan también los errores evaluados a nivel de serie con la eficiencia NS y el coeficiente de correlación R2. La bondad de la aproximación puede considerarse entre Excelente y Buena para sitios de PSM, ROS, VCO, SNI y RAM y Regular para SPE.

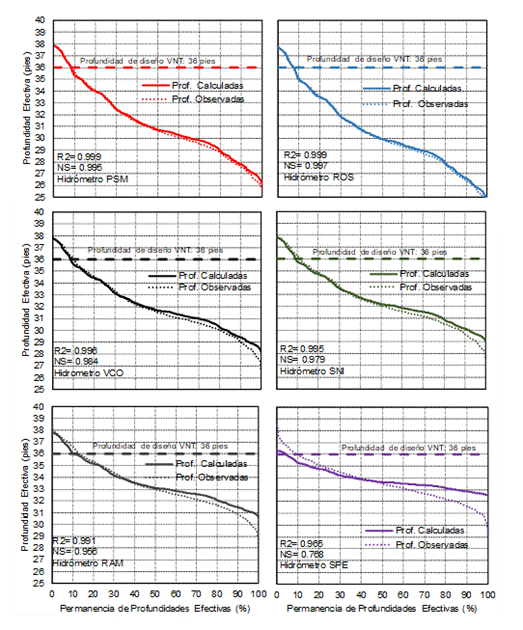
Figura 11. Permanencia de Profundidades Efectivas en los sitios de los Hidrómetros.

A modo de resumen para una visualización integral del tramo en estudio se presenta en la Figura 12 el perfil longitudinal del fondo del río en el eje de la VNT, el fondo de diseño de la VNT, los perfiles longitudinales hidráulicos de los niveles máximos y mínimos observados y simulados en el trienio de la bajante y de los niveles referencia de la VNT (80% de permanencia), la ubicación de los hidrómetros y los pasos críticos y los anchos del cauce del río. Se constata, tanto a partir de los niveles observados como de los simulados, que los 36 pies de la profundidad de proyecto de la VNT pudieron asegurarse en los pasos críticos solo durante la presentación de niveles cuyas permanencias en cada hidrómetro son inferiores al 10% del tiempo total de la bajante.

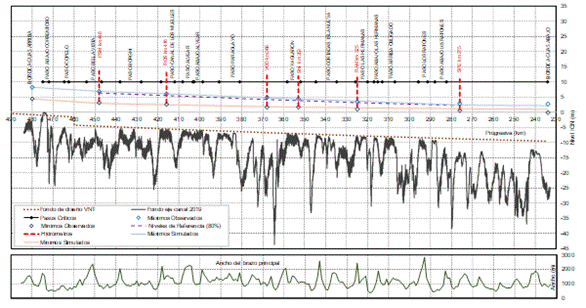
Figura 12. Perfil longitudinal del fondo del río en eje de la VNT, fondo de diseño de la VNT, perfiles hidráulicos máximo y mínimo y de referencia, ubicación de hidrómetros y pasos críticos y anchos del cauce del río.

Definición de módulo de velocidades integradas en la vertical

A manera ilustrativa se presenta la potencialidad del modelo para genera campos areales del modulo de la velocidad integrada en la vertical. Si bien no se cuentan con aforos con los que se puede constatar la bondad del ajuste entre velocidades observadas y simuladas durante el período de la bajante, se muestran como ejemplos, las velocidades computadas para caudales cercanos a los extremos observados en un tramo cercano a ROS (km 416). La Figura 13(a) corresponde a un caudal circulante de 16000 m³/s y la Figura 13(b) corresponde a un caudal circulante de 6800 m³/s. Si bien no pueden emplearse los mapas de modo cuantitativo, puede verse claramente con los tonos de colores de los contornos rellenos el contratse entre los campos de velocidades de caudales tan disímiles.

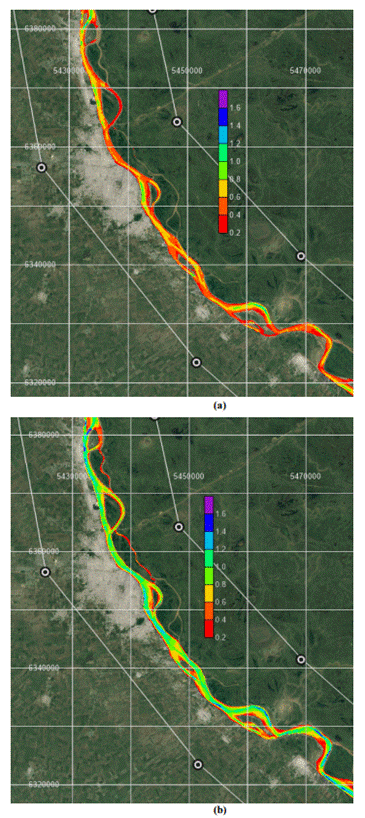
Figura 13. Campo de velocidades (m/s) integradas en la vertical en km 416. (a) Q = 6000 m³/s y (b) Q = 16000 m³/s

RESULTADOS Y DISCUSIÓN

Permanencias de niveles hidrométricos extremos

Se presenta a continuación el análisis de permanencias de niveles extremos en los 4 sitios donde se evidenció el mejor comportamiento del modelo en su utilización como predictor. En la Figura 14 se presentan las permanencias de las series de niveles y niveles máximos y mínimos e histogramas observados y simulados y nivel de referencia de la VNT, tanto para la serie completa de niveles como para la serie moderna (1972-2022) en PSM, ROS, VCO y SNI. Además, se presentan los histogramas de frecuencias relativas de los niveles dentro del trienio de la bajante. En la Tabla 5 se presentan la permanencias observadas y simuladas.

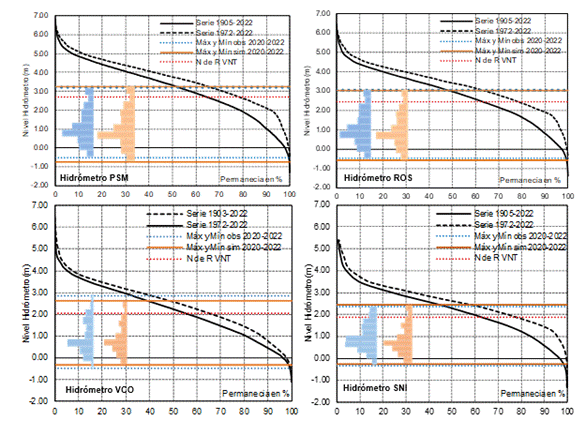
Figura 14. Permanencias de las series de niveles y niveles máximos y mínimos e histogramas observados y simulados y nivel de referencia de la VNT.

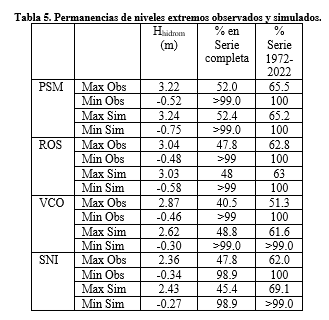
En PSM el máximo nivel observado corresponde al 52% de permanencia en la serie de niveles completa (1905-2022) en tanto que en la serie moderna (1972-2022) se asocia a un 65.5% de permanencia. En lo que concierne a los valores simulados las permanencias resultaron de 52.4% y 65.2% (errores absolutos menores al 0.4%). En niveles mínimos observados, el menor corresponde a >99% y 100% de permanencia en la serie completa y en la moderna respectivamente. Por otro lado, en niveles mínimos simulados, las permanencias son idénticas a las correspondiente a mínimos observados.

En ROS el máximo nivel observado corresponde al 47.8% de permanencia en la serie de niveles completa (1884-2022) en tanto que en la serie moderna (1972-2022) se asocia a un 62.8% de permanencia. En lo que concierne a los valores simulados las permanencias resultaron de 48.0% y 63.0% (errores absolutos menores al 0.2%). En niveles mínimos observados y simulados se da el mismo comportamiento que en el caso de PSM.

En VCO el máximo nivel observado corresponde al 40.5% de permanencia en la serie de niveles completa (1904-2022) en tanto que en la serie moderna (1972-2022) se asocia a un 51.3% de permanencia. En lo que concierne a los valores simulados las permanencias resultaron de 48.8% y 61.6% (errores absolutos menores a 9.7%). En niveles mínimos observados y simulados se da el mismo comportamiento que en el caso de PSM y ROS.

En SNI el máximo nivel observado corresponde al 47.8% de permanencia en la serie de niveles completa (1905-2022) en tanto que en la serie moderna (1972-2022) se asocia a un 62.0% de permanencia. En lo que concierne a los valores simulados las permanencias resultaron de 45.4% y 69.1% (errores absolutos menores a 7.1%). En niveles mínimos observados y simulados se da el mismo comportamiento que en el caso de PSM, ROS y VCO.

Se concluye que las determinaciones de las permanencias a partir de los niveles simulados, tienen una elevada coincidencia con los niveles observados en PSM y ROS y muy buena coincidencia en VCO y SNI.

Además de la observación de los histogramas de frecuencias relativas puede demostrarse que el intervalo de clase donde se dieron las mayores valores de frecuencia han coincidido entre las series de valores observados y simulados.

Al contrastar los niveles observados con el nivel de referencia, puede inferirse que durante la bajante, los niveles hidrométricos del río se situaron en promedio un 90.6% de los días por debajo de los niveles de referencia establecidos para el diseño de la VNT. A partir de valores de permanencias de los niveles se reafirma la severidad de la bajante observada en el río Paraná durante el trienio 2020-2022.

En la Figura 15 se presenta en el subtramo del río entre PSM y SNI, el rango de oscilación de los niveles observados y calculados (por razones de escala de representación la diferencia es imperceptible en la figura) en el trienio 2020 a 2022 y los niveles extremos observados en la serie completa de niveles desde 1904 a 2022 y en la serie moderna desde 1972 a 2022, conjuntamente con el perfil del fondo en el eje de la VNT en 2019. La representación permite una mirada adicional acerca de la rigurosidad de los niveles registrados en la bajante en relación a sus extremos históricos.

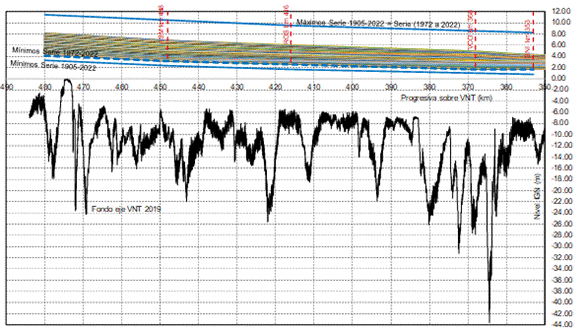
Figura 15. Rango de Niveles en trienio 2020-2022 y Extremos en Series (1904-2022) y (1972-2022) en subtramo desde PSM a SNI.

Curvas H-Q observadas y simuladas

Un tópico de interés al plantear la comparación entre niveles observados y simulados, tanto de la calibración como de la explotación del modelo como predictor, es en función de las relaciónes altura-caudal en cada uno de los sitios de los hidrómetros.

En las Figuras 16 y 17 se presentan las relaciones H-Q entre los niveles hidrométricos y los caudales observados y simulados. Se aclara que solo se contó con caudales observados en el sitio de PSM, en el resto de los sitios se asumió que el caudal observado es igual al simulado durante la etapa de calibración.

La Figura 16 corresponde a las curvas H-Q originadas en la calibración donde se impusieron niveles en función del tiempo en ambos bordes. Puede observarse claramente que a medida que avanzamos hacia aguas abajo las relaciones tanto en valores observados como simulados tiene una notable dispersión en relación a un planteo de biunicidad. Precisamente, tal como se mencionara anteriormente, los forzantes de niveles en el borde aguas abajo propagan su efecto hacia aguas arriba, pudiéndose evidenciar que solamente en ROS y PSM no cobra demasiado importancia la propagación de la perturbación en el borde abajo.

La Figura 17 corresponde a las curvas H-Q originadas en la explotación del modelo como predictor. Se evidencia que la biunicidad de las relaciones entre H y Q que se fuerzan aguas abajo se propagan hacia aguas arriba. La imposición de la condición de borde aguas abajo que le otorga al modelo capacidades como predictor, hace que la modelación pierda bondades de cálculo en la región cercana al borde aguas abajo.

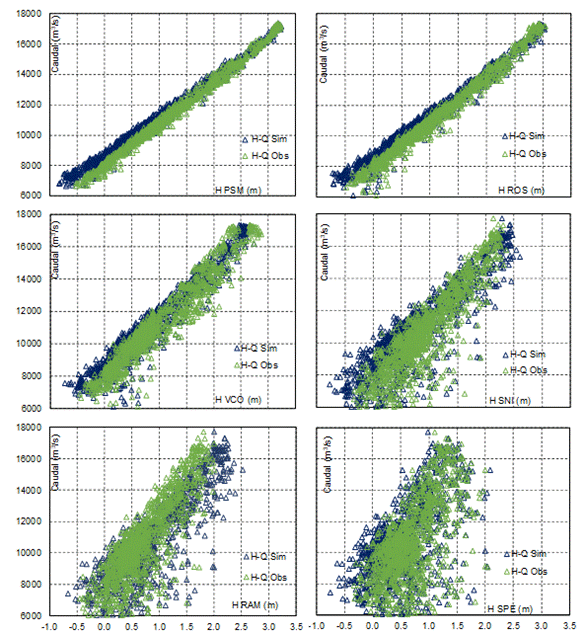
Figura 16. Relaciones H-Q en calibración con imposición de condiciones de borde H(t) y H(t).

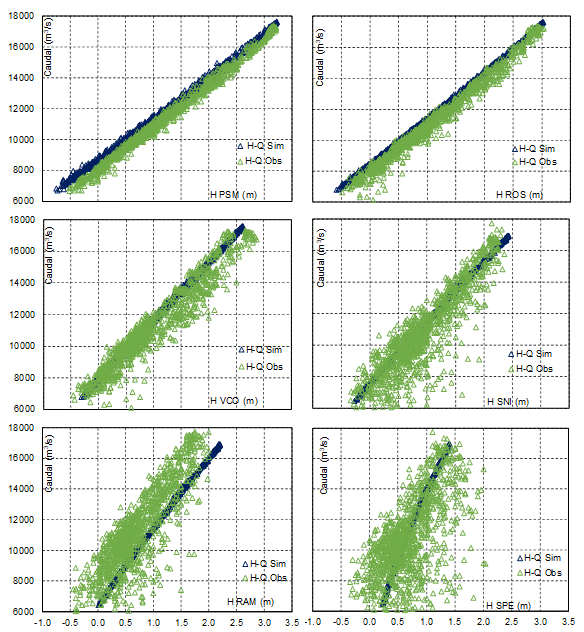
Figura 17. Relaciones H-Q en explotación del modelo como predictor con imposición de condiciones de borde Q(t) y H-Q.

CONCLUSIONES

La estadística descriptiva de los niveles hidrométricos observados en el trienio 2020 a 2022 sin lugar a dudas ratifica que se trató de una de las más severas bajantes del río Paraná desde que se realizan mediciones. Si se analizan los niveles en las curvas de permanencias (ocurrencias de niveles mayores o iguales) se evidencia que los niveles observados entre 2020 a 2022 en el decil de mayor frecuencia relativa con respecto a las curvas de permanencias de la serie completa (1904 a 2022), se determina en las estaciones PSM, ROS, VCO y SNI un valor promedio de 89% y si comparamos con la serie contemporánea (1972-2022) la permanencia asociada al grupo de niveles del decil de mayor frecuencia relativa es de 97%.

En lo referente a la calibración del modelo de simulación hidrodinámica de baja complejidad empleado, se ha logrado aproximar la mejor respuesta del mismo, en un escenario en que se incorporan en ambos bordes las condiciones H(t) observadas, con un coeficiente de Manning uniforme en todo el tramo e igual a η = 0.029 s/m^1/3. Al tratarse de un modelo simplificado de baja complejidad en sus ecuaciones gobernantes, el coeficiente de resistencia encapsula parcialmente y en forma aproximada otros mecanismos que no son debidamente contemplados por las ecuaciones gobernantes simplificadas.

Los ajustes de limnigramas han sido Muy Buenos en todos los sitios de los hidómetros PSM, ROS, VCO, SNI, RAM y SPE. Se evidencia en todas las estaciones de aforos que los mínimos simulados son inferiores a los observados y en menor medida los máximos simulados son mayores a los observados en las 3 estaciones aguas abajo (SNI, RAM y SPE).

Cuando se realiza el análisis de sensibilidad del coeficiente de Manning ajustado, los niveles de agua no cambian significativamente debido a los forzantes impuestos a los mismos en los bordes aguas arriba y abajo, en cambio, varía el caudal intercambiado. En el escenario calificado como de mejor ajuste, los caudales generados internamente en PSM por el modelo para 0.027 s/m^1/3 ≤ η ≤ 0.032 s/m^1/3 establecieron una franja valores que incluyen el 97% de los caudales calculados por el SNIH (2023), caudales aforados por SNIH (2023) y los determinados por Basile y Riccardi (2023).

Se evidencia un factor no menor que influye fuertemente en la condición de borde aguas abajo, que es la oscilación de niveles debido al ciclo diario de mareas y las alteraciones aleatorias no regulares de niveles por oleaje y tormentas en el río de la Plata. Sin dudas, este modelo no describe con sus ecuaciones los mecanismos hidrodinámicos adicionados y además el introducir la condición de borde cada 24 hs, tampoco permite reproducir las perturbaciones y su propagación hacia aguas arriba de las variaciones subdiarias de niveles. Esto hace que el ajuste vaya descendiendo en su calidad desde el sitio VCO hacia aguas abajo.

No obstante, en la calibración cuando se comparan las curvas H-Q observadas y simuladas el ajuste puede considerarse entre Muy Bueno y Bueno en todas las estaciones de comparación.

En la evaluación del modelo como herramienta de predicción, se lo alimentó con el hidrograma de caudales medios diarios generado con el mejor ajuste logrado en la calibración e imponiendo en el borde aguas abajo una condicón H-Q biunívoca resultante de múltiples pruebas de aproximación. Puede verificarse que la relación entre niveles y caudales observadas en el borde abajo se aleja de forma importante de una relación biunívoca y esto no lo puede representar el modelo por lo que, los resultados en términos de niveles de agua en las estaciones de SPE y RAM no son buenos. En la comparación de limnigramas las bondades de la aproximación pueden calificarse como Muy Buenas entre el borde aguas arriba (km 480) y SNI (km 353), Aceptables en RAM (km 325) y Pobres en SPE (km 276) y en el borde aguas abajo (km 232).

La elección de la curva H-Q en el borde aguas abajo constituyó una variable de ajuste para el uso del modelo como herramienta de predicción. En este sentido, fueron evaluadas diferentes relaciones y hasta una relación H(t) constante, adoptándose la que menor error de niveles provocaba en las estaciones cercanas al borde aguas abajo. Resulta pertinente mencionar que si bien la influencia de la curva H-Q en el borde aguas abajo se atenúa hacia aguas arriba, el modelo computó pequeñas variaciones de niveles, propagadas hasta PSM. Se evidencia que, al fijar como condición de borde aguas abajo en el km 232 una relación H-Q, el modelo gana capacidad como predictor pero pierde calidad en la reproducción de los niveles observados en la región cercana al borde.

Otra característica que ha resultado satisfactoria cuando se procesan los niveles calculados en la modelación, es el establecimiento de las permanencias de los mismos y su comparación con las permanencias observadas. Se destaca que la proyección de las permanencias de niveles ante una determinadas señal de entrada al tramo resulta de importancia para la planificación entre otras de la navegación comercial. En este sentido, la permanencia de las profundidades efectivas en la VNT como los histogramas de frecuencias relativas de los niveles en el trienio, fueron considerados entre Excelentes a Buena desde PSM a RAM y Regular en SPE.

El problema introducido por la condición de borde aguas abajo puede mejorarse considerando el traslado hacia aguas abajo y lo óptimo será hasta el río de la Plata (como se reporta por otros autores en trabajos antecedentes con modelos unidimensionales). No obstante a partir del km 232 el río se bifurca en el Paraná de las Palmas y el Paraná Guazú y otros cauces, por lo que todo esto involucrará una sustancial complejización del escenario de modelación.

En lo que concierne a la hipótesis de bifurcación de escurrimiento planteada en el río Pavón considerando una derivación de 3 al 5% de caudal, fue verificada indirectamente y es considerada adecuada. No obstante, debe ser verificada con información generada en mediciones.

Una cuestión que amerita una próxima consideración tanto en el MDE del fondo del cauce como en las proyecciones a cotas IGN de los niveles, es la posible corrección de los ceros de los hidrómetros a partir de lo presentado en la página del Instituto Nacional del Agua (INA) (s.f.) y también en INA (2018). En este trabajo no se han considerado las correcciones por detectarse en algunos casos, importantes diferencias con estudios antecedentes.

En una síntesis del trabajo realizado podemos concluir que, la herramienta de simulación se proyecta con capacidad para ser implementada en la estimación de niveles de agua y profundidades efectivas disponibles en la VNT, en posibles evaluaciones de escenarios futuros donde se disponga de la predicción de caudales entrantes al tramo en un determinado período, de modo de aportar a la mejor gestión sustentable posible de (i) la operación de obras de tomas de agua y volcamiento de efluentes; (ii) el funcionamiento de estructuras portuarias; (iii) la previsión de las restricciones del transporte fluvial y (iv) la mitigación de los impactos negativos sobre los ecosistemas presentes y la biodiversidad constitutiva de los humedales.

AGRADECIMIENTOS

Los autores desean expresar su agradecimiento a la UNR por el apoyo brindado en el marco de los PIDs 80020190300002UR y 80020190300073UR y a la DNVN-DPI por los datos topobatimétricos e hidrométricos facilitados.

REFERENCIAS

Basile, P. A. y Riccardi, G. A. (2002). A Quasi-2D Hydro-Morphological Mathematical Model: An Application to the Argentinean Paraná River. International Journal of Sediment Research, 17 (1), 20-30.

Basile, P. A. y Riccardi, G. A. (2023). Análisis de caudales del río Paraná y contextualización de las bajantes en los años hidrológicos 2019/20, 2020/21 y 2021/22. Cuadernos del CURIHAM, Edición Especial (2023): Bajante del río Paraná. e01. https://doi.org/10.35305/curiham.ed23.e01

Basile, P. A., Riccardi, G. A., Garcia, M. L. y Stenta, H. R. (2007). Quasi-2D modeling of hydro-sedimentological processes in large lowland river-floodplain systems. Workshop on Morphodynamics Processes in Large Lowland Rivers. Santa Fe, Argentina.

Basile, P. A., Riccardi, G. A., Peruzzo, F. C. y Trivisonno, F. (2015). Modelación Hidrodinámica de un Tramo del Río Paraná Inferior. Séptimo Simposio Regional sobre Hidráulica de Rios, Montevideo, Uruguay.

Basile, P. A., Riccardi, G. A., Peruzzo, F. C. y Garcia, M. L. (2016). Modelación Hidrodinámica Bidimensional del río Paraná Inferior. Revista Aqua-LAC, Vol. 8, Nº 2, pp. 1-13. ISSN 1688-2873.

Bombardelli, F. A., Menéndez, A. N., Brea, J. D., Lapetina, M. R. y Uriburu Quirno, M. (1994). Estudio hidrodinámico del Delta del río Paraná mediante modelación matemática. Informe LHA-INCyTH 137-03-95, Ezeiza, Argentina.

Borús, J. y Sabarots Gerbec, M. (2015). Caracterización de Niveles Mínimos en la Vía Navegable del río Paraná. XXV Congreso Nacional del Agua, Paraná, Argentina.

Dirección Nacional de Vías Navegables Delegación Paraná Inferior (2014). Cartografía de río Paraná. Datos topobatimétricos tramo km 234 – 480. Comunicación institucional. Rosario, Argentina.

Dirección Nacional de Vías Navegables Delegación Paraná Inferior (2023). Planilla de Alturas en hidrómetros de tramo Paraná Inferior. Comunicación institucional. Rosario, Argentina.

Facultad de Ingeniería y Ciencias Hídricas (2006). Estudios Complementarios Hidráulicos y Morfológicos de la Zona de la Isla de la Invernada. Informe final. UNL. Santa Fe, Argentina.

Garcia, M. L., Basile, P. A., Riccardi, G. A. y Rodriguez, J. F. (2015). Modelling extraordinary floods and sedimentological processes in a large channel-floodplain system of the Lower Paraná River (Argentina). International Journal of Sediment Research, 30 (2015), 150-159.

Garcia, M. L., Basile, P. A. y Riccardi, G. A. (2017). Estudio de Aforos y Modelación Hidro-sedimentológica del Cauce y Planicie Aluvial del río Paraná. VIII Simposio Regional sobre Hidráulica de Ríos. Córdoba. Argentina.

Guizzardi, S., Bianchi, J., Cortese, J., Uriburu Quirno, M. y Sabarots Gerbec, M. (2022). Forecast System Implementation in the Paraná Delta. Proceedings of the 39th IAHR World Congress 19-24 June, Granada, Spain.

Instituto Nacional del Agua (2018). Informe LHA 02-373-18. Campaña de relevamiento de ceros hidrométricos Delta Paraná. Estudio hidrodinámico integrador del Delta del río Paraná con fines múltiples. Ezeiza, Argentina. 133p. https://www.ina.gob.ar/delta/pdf/03_02_INA-DELTA_Info04_CerosHidrometricos.pdf

Instituto Nacional del Agua (s.f.). Estudio hidrodinámico integrador del Delta del río Paraná con fines múltiples. https://www.ina.gob.ar/delta/index.php?seccion=4

Morale, M., Sabarots Gerbec, M. y Garcia, P. (2020). A Hydrodinamic Model as Input for a Spatial Planning Tool. Case Study: Delta of the Paraná River (Argentina). Proceedings of the 1st IAHR Young Professionals Congress. Spain Water and IWHR China.

Nicholas, A. P., Sandbach, S. D., Ashworth, P. J., Amsler, M. L., Best, J. L., Hardy, R. J., Lane, S. N., Orfeo, O., Parsons, R., Reesink, A. J. H., Sambrook Smith, G. H. y Szupiany, R. N. (2012). Modelling hydrodynamics in the río Paraná, Argentina: An evaluation and inter-comparison of reduced complexity and physics based models applied to a large sand-bed river. Geomorphology, 169–170, 192–211.

Peruzzo, F., Riccardi, G. A., Basile, P. A. y Garcia, M. L. (2016). Simulación cuasi-2d en cauce principal del tramo Paraná inferior km 234-480. IFRH 2016, Ezeiza, Argentina. 13p.

Peruzzo, F., Riccardi, G. A., Basile, P.A. y Garcia, M. L. (2017). Evaluación de un modelo hidrodinámico bidimensional en un tramo del cauce principal del río Paraná. VIII Simposio Regional sobre Hidráulica de Ríos. Córdoba. Argentina.

Re, M., Sabarots Gerbec, M. y Storto, L. (2015). Estadística de niveles en el Delta del río Paraná mediante modelación hidrodinámica. VII Simposio Regional sobre Hidráulica de Ríos, Montevideo, Uruguay.

Riccardi, G. A. (2000). A cell model for hydrological-hydraulic modeling. Journal of Environmental hydrology, 8, pp. 1–13. http://www.hydroweb.com/jeh/jeh2000/riccardi.pdf

Riccardi, G. A. y Basile, P. A. (2023). Análisis de Perfiles Hidráulicos en El Tramo km 232-480 del río Parana durante la Bajante 2020-2022. XVII Jornadas de Ciencia, Tecnología e Innovación. UNR, Rosario, Argentina. https://jornadasctei.unr.edu.ar/analisis-de-perfiles-hidraulicos-en-el-tramo-km-232-480-del-rio-parana-durante-la-bajante-2020-2022/

Riccardi, G. A., Basile, P. A., Peruzzo, F. y Garcia, M. L. (2022). Actualización de la Simulación Hidrodinámica de la Bajante en el río Paraná en el tramo km 232-480. XVI Jornadas de Ciencia, Tecnología e Innovación UNR. Rosario, Argentina. https://jornadasctei.unr.edu.ar/actualizacion-de-la-simulacion-hidrodinamica-de-la-bajante-en-el-rio-parana-en-el-tramo-km-232-480/

Sabarots Gerbec, M. (2014). Estudio de la dinámica superficial de la red de canales del Delta Medio del río Paraná. IFRH 2014, 2do. Encuentro de Investigadores en Formación en Recursos Hídricos. Instituto Nacional del Agua, Ezeiza, Argentina.

Sabarots Gerbec, M. y Borús, J. (2016). Caracterización Hidrodinámica en aguas bajas para la Vía Navegable del río Paraná. IX Congreso Argentino de Ingeniería Portuaria, Buenos Aires, Argentina.

Sabarots Gerbec, M., Re, M., Storto, L. y Morale, M. (2018). Análisis de Repartición de Caudales en Bifurcaciones del Delta del río Paraná. XXVII Congreso Latinoamericano de Hidráulica. Buenos Aires, Argentina.

Servicio de Hidrografía Naval (2018). Base de Datos Digital de Cartas Náuticas de río Paraná Inferior. http://www.hidro.gov.ar/cartas/cartasnauticas.asp. Cartas Náuticas descargadas en año 2018.

Sistema Nacional de Información Hídrica (2023). Base de Datos del Sistema Nacional de Información Hídrica, Secretaria de Infraestructura y Política Hídrica, Ministerio de Obras Públicas. https://snih.hidricosargentina.gob.ar

Subsecretaria de Puertos, Vías Navegables y Marina Mercante (2020). Relevamientos Batimétricos Canal de Navegación, Ministerio de Transporte. https://www.argentina.gob.ar/transporte/puertos-vias-navegables-y-marina-mercante. Relevamientos batimétricos en vía de navegación troncal descargados en año 2020.

Stenta, H., Rentería, J. P. y Riccardi, G. A. (2005). Plataforma computacional para gestión de información en la simulación hidrológica-hidráulica del escurrimiento superficial. XX Congreso Nacional del Agua, Mendoza, Argentina, 1, T74, 13p.

Wilson, M., Bates, P., Alsdorf, D., Forsberg, B., Horritt, M., Melack, J., Frappart, F. y Famiglietti, J. (2009). Modeling large-scale inundation of Amazonian seasonally flooded wetlands. Geophysical Research Letters, 34 (2007), pp. L15404. 1029/2007GL030156. hal-00442256.

Trabajo recibido el 02/02/2024, aceptado por el Consejo Editorial para su publicación el 16/02/2024 y publicado el 26/02/2024.

COMO CITAR

Riccardi, G. A. y Basile, P. A. (2024). Modelación hidrodinámica en el tramo km 232-480 del río Paraná durante la bajante 2020 a 2022. Cuadernos del CURIHAM, Edición Especial (2023): Bajante del río Paraná. e03. https://doi.org/10.35305/curiham.ed23.e03

ROLES DE AUTORÍA

GR y PB realizaron en conjunto el proceso de investigación, recopilación de datos, análisis, conceptualización y completaron la preparación, creación y redacción del trabajo. PB contribuyó en la concepción de la idea; GR contribuyó en el diseño del estudio, recolección, análisis e interpretación de los datos. Ambos aprobaron la versión para ser publicada y son capaces de responder respecto a todos los aspectos del manuscrito.

LICENCIA

Este es un artículo de acceso abierto bajo licencia: Creative Commons Atribución -No Comercial -Compartir Igual 4.0 Internacional (CC BY-NC-SA 4.0) (https://creativecommons.org/licenses/by-nc-sa/4.0/deed.es)

Este trabajo se enmarca dentro de la EDICIÓN ESPECIAL (2023): Bajante del río Paraná de la revista Cuadernos del CURIHAM