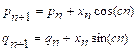DOES DETERMINISM IMPLY CAOS IN HYDROLOGICAL VARIABLES?
¿EL DETERMINISMO
IMPLICA CAOS EN VARIABLES HIDROLOGICAS?
Sebastián
Marotta(1)(2)(3)(*), Raúl Rivas (1)(3), Cristian Guevara Ochoa (1)(4) y María Florencia Degano
(1)(4)
(1)
Instituto de Hidrología de Llanuras. Azul, Buenos Aires, Argentina.
(2) Universidad
Argentina de la Empresa. Instituto de Tecnología. Buenos Aires, Argentina.
(3) Comisión
de Investigaciones Científicas de la Provincia de Buenos Aires. Buenos Aires,
Argentina.
(4) Consejo
Nacional de Investigaciones Científicas y Técnicas. Argentina.
(*) e_mail: smmarotta@gmail.com
ABSTRACT
In this paper we present several
hydrological time series from Argentina that include, evapotranspiration,
precipitation, and stream flow. We survey previous results and apply the 0-1
test for chaos to classify the sequences as regular or chaotic. Previous
studies have shown evidence of chaos in several observables from hydrology
using the traditional phase space reconstruction method and the computation of
Lyapunov exponents. The 0-1 test for chaos can be used as a first step to
identify the type of time series, that later can be subjected to the more
detailed analysis of the phase space reconstruction. Assuming that the systems
that generated these time series are deterministic, the 0-1 test for chaos
classifies all of them as chaotic.
Keywords: Hydrology,
Time series, 0-1 test for chaos, Evapotranspiration, Precipitation.
RESUMEN
En este artículo presentamos varias series
de tiempo hidrológicas de Argentina que incluyen, evapotranspiración,
precipitación y caudales. Revisamos previos resultados y aplicamos el test 0-1
de caos para clasificar las secuencias como regulares o caóticas. Estudios
previos han demostrado evidencia de caos en muchos fenómenos hidrológicos
usando el método tradicional de la reconstrucción del espacio de fase y el
cálculo de exponentes de Lyapunov. El test 0-1 de caos puede ser usado como un
primer paso para identificar el tipo de serie de tiempo, y que luego puede ser
sujeta al análisis más detallado de la reconstrucción del espacio de fase. Si
asumimos que los sistemas que generaron estas series de tiempo son
determinísticos, el test 0-1 de caos las clasifica a todas ellas como caóticas.
Palabras
clave: Hidrología, Series de
tiempo, Test 0-1 de caos, Evapotranspiración, Precipitación.
INTRODUCTION
The hydrologic cycle is a large feedback
loop that determines the conditions of water on Earth globally and locally, and
with strong interactions between different systems at different spatial and
temporal scales. The natural phenomena involved in the water cycle are
described by physical laws and mathematical models that can explain many
aspects at the microscopic and macroscopic levels, and are, in general,
represented by nonlinear systems. The water cycle gathers all kinds of
materials, fluids, gases, and solids, as well as organic elements with specific
characteristics and properties that change with time. On the one hand, there
are several external factors that have a periodic nature and are present in
these systems, like the ones related to the motion of the Earth around the Sun,
the rotation of the Moon around the Earth, and the rotation of the Earth about
its axis, among others. These phenomena are responsible for the annual,
seasonal, and daily periodic variations found in several hydrological
components. On the other hand, the atmospheric agents like temperature, winds,
clouds, precipitation, and the local topography and vegetation of the basins
imply that the variables, like precipitation or flow discharge, are affected by
many other variables in an irregular manner. These conditions represent a
challenge for the meteorologist as well as for the hydrologist when trying to determine
the state of a part of the system during a specific period of time. The
relationship between the different interconnected systems at different scales
in space and time is not completely understood.
Chaos theory gives a
frame for the study of deterministic systems that present seemingly stochastic
behavior and are unpredictable in the long-term. The three main ingredients of
chaotic systems are, periodic behavior (regularity), sensitive dependence on
initial conditions (unpredictability), and mixing (indecomposabiliy), see
(Devaney, 2003). In the last few decades these properties were studied in
several mathematical models, laboratory experiments and also natural phenomena,
see for example, (Tsonis, 1992; Turcotte, 1997; Schreiber, 1999; Kantz and Schreiber,
2004; Sivakumar and Berndtsson, 2010; Tsonis, 2007; Skokos et al., 2016).
Several techniques have been applied to the
study of hydrological time series with many different outcomes. Some
researchers consider that the time series that correspond to some of these
hydrological variables may be better understood when interpreted as generated
by stochastic processes, and many times the predictions of stochastic models
are in good agreement with the observed phenomena. For a discussion of some
aspects of these interpretations see (Koutsoyiannis, 2006). Others instead,
take a deterministic approach, and in some cases their predictions in the short
term may be more accurate than the ones obtained with stochastic models. In
2017, Professor Sivakumar published the first book about chaos in hydrology
(Sivakumar, 2017), where the different approaches are described, and the
chaotic approach selected from a pragmatic point of view, with the
interpretation that chaos theory can bridge the gap between stochasticity and
determinism. The book is full of excellent ideas and applications, and shows
the results of experiments that many researchers around the world have obtained
in the study of hydrological variables. Some of the methods discussed in
Sivakumar (2017) involve the phase space reconstruction, the computation of the
correlation integral, the computation of Lyapunov exponents, and the study of
return maps. The method of phase space reconstruction has been applied to
several hydrological phenomena in the past few decades, see for example
(Sivakumar, 2017; Pasternack, 1999; Sivakumar, 2000a; Sivakumar, 2002b; Sivakumar-
Jayawardena, 2002; Sivakumar and Jayawardena, 2002; Sivakumar, 2004; Sivakumar
and Berndtsson, 2005) and references therein.
In 2004, Gottwald and Melbourne (2004)
developed a method to differentiate deterministic periodic or quasi-periodic
time series from chaotic ones, using the 0-1 test for chaos. In this test, we
compute a parameter K that gives a value close to 0, if the behavior of the
system is regular, and a value close to 1, if the behavior is chaotic. The 0-1
test for chaos is based on sophisticated mathematics that relate group
extensions and dynamics. The test was improved in the following years and has
been applied to mathematical systems, laboratory measurements and also natural
observables, see (Gottwald and Melbourne, 2005; Falconer et al., 2007; Gottwald and Melbourne, 2009a; Gottwald and Melbourne,
2009b; Gottwald and Melbourne, 2016). For a pedagogical overview of the
mathematics behind the test see (Bernardini and Litak, 2016). In some cases,
the test has also been shown to perform better than the traditional methods
using phase space reconstruction and Lyapunov exponents, when the time series
is contaminated with noise, see (Gottwald and Melbourne, 2016). Applications of the 0-1 test in physics, finance,
and oceanography can be found in (Lugo-Fernandez, 2007; Litak et al., 2009a; Litak et al., 2009b; Krese and Goverkar, 2012;
Chowdhury et al., 2012; Zachilas and
Psarianos, 2012; Xin and Li, 2013; Prabin Devi et al., 2013; Krese and Govekar, 2013; Kriz and Kratochvil, 2014; Kriz,
2014). In particular, we found two applications to hydrological variables
related to river flows and runoff time series in (Li et al., 2014; Kedra, 2014). Kedra (2014) used the 0-1 test and the
phase space reconstruction approach.
The more traditional method of deciding if
a time series is chaotic by reconstructing the phase space, finding the
correlation dimension, and measuring Lyapunov exponents is very demanding in
terms of computing. Each of the several steps necessary to obtain the
information requires large computations and specific considerations that need
careful analysis. On the other hand, the phase space reconstruction approach
gives a more detailed description of the system like, for example, the minimum
number of variables necessary to describe the behavior of the system in phase
space. Then, the variables may be used to create a model of the system, and
perform short term forecasts.
The 0-1 test has the advantage of being
easy to program and work with, and takes short computation time. The test works
directly with the time series and the classification is independent of the
dimension of the underlying dynamical system under investigation, as well as,
independent of the system being continuous (differential equations) or discrete
(maps). This is a major difference with respect to the phase space
reconstruction approach where the time series is considered the sample of a
continuous variable, and where the dimension of the appropriate phase space of
the system has to be determined in order to obtain the Lyapunov exponents to
classify the system as chaotic.
As with any other test, it is necessary to
use caution when applying it. Some of the problems that may arise due to
oversampling continuous dynamical systems are discussed in (Melosik and
Marszalek, 2016). We remark that the 0-1 test for chaos works assuming that the
time series was generated by a deterministic system, and it is not relevant to test
sequences generated with stochastic systems, see for example (Hu et al., 2005; Gottwald and Melbourne, 2008)
for a discussion about this issue.
Methods to evaluate the evidence of chaos
from a time series also require that the time series is sufficiently long to
capture all aspects of the dynamics. It is not possible to assert if a natural
time series of finite length has this property. For time series that may be too
short to allow for convergence of K to either 0 or 1, strong indications for
the behavior (regular or chaotic) can be found by looking at the values of K as
a function of the length of the time series.
The application of any technique to
analyze, describe, and ultimately perform forecasts depend on the
characteristics of the system under study. If the system is considered
stochastic, then several techniques are available for its study. When the
system is considered deterministic and does not show signs of chaotic behavior,
the analysis, description, and forecast (in the short and long term) are performed
through modeling using differential equations. Finally, when the system is
considered deterministic and shows signs of chaotic behavior, the study is of a
different nature. Long term forecast is not available in these types of
systems. The goal is to use the time series to reconstruct a chaotic attractor
in phase space, which can provide a numerical model for the dynamics of the
system and can be used for short term forecast, as seen, for example, in (Kedra,
2014). The reconstruction of the attractor is a long and difficult process that
may take several months or years to perform, even when a long time series is
available. Therefore, it is of great advantage to have a test, like the one
described in these notes, to first classify the system as chaotic before considering
such a demanding task.
In this paper we analyze several
hydrological time series from Argentina that include evapotranspiration,
precipitation, and stream flow. We anticipate that all of these time series are
classified as chaotic by the 0-1 test. The method provides the hydrologist with
a first tool for the identification of chaotic behavior that later can be
refined through the use of more detailed and elaborate approaches, like for
example, the phase-space reconstruction method, the computation of Lyapunov
exponents, the analysis of return maps, and others.
In order to illustrate the method and
compare the results, we apply the test to time series derived from the Lorenz
system and the quadratic map. See Figures 1 and 2. These systems have been
widely studied numerically and theoretically, and their main properties are
well known, see for example, (Devaney-2003, Lorenz-1963). For the quadratic map
we show one regular and one chaotic orbit.
DATA AND METHODS
Lorenz’s system.
The Lorenz system (Lorenz, 1963) is
a simplified model for the phenomenon of convection in fluid dynamics. It is a
continuous system of three ordinary differential equations with three
parameters given by
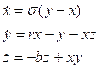 (1)
(1)
where the dot denotes the time
derivative of the variable with respect to time. The typical trajectories that
are solutions of the Lorenz system are bounded and converge to a strange
attractor in phase space. The solutions behave in a non-periodic fashion and
the system shows sensitive dependence on initial conditions, that is, the
system presents chaotic dynamics for certain values of the parameters. In
particular, we use the classical values σ=10,
r=28 and b=8/3. We consider the Lorenz system as a prototypical example of a
continuous chaotic dynamical system with a strange attractor. Figure 1 shows
the time series of the x variable and
the trajectory of a solution in phase space.
The quadratic map
The quadratic family of
functions f(x)=x2+µ with parameter µ, regarded as a map of the form xn+1=xn2+ µ, is a feedback system that presents
chaotic behavior for some values of the parameter µ. It is one of the simplest nonlinear differentiable maps in one
dimension, and we use it as a prototype of a discrete chaotic dynamical system,
as well as, to test for a regular orbit.
Figure 2 shows two time
series corresponding to regular and chaotic behavior, and the orbit diagram.
The orbit diagram shows the long term behavior of a typical orbit, and the
period-doubling bifurcation route to chaotic behavior characteristic of this
type of map (Devaney, 2003). We can see that the value of µ =-1.3 corresponds to an attracting limiting cycle of period 4,
and that a value of µ =-2 corresponds
to chaotic behavior. Since theoretical results are well known for the quadratic
map, we use the 0-1 test on these two sequences for illustration and comparison
to the behavior of the other variables.
Figure
1. On the left, we see a trajectory of the Lorenz system in phase space, see equation
(1). Orbits are attracted to a strange attractor, and go around two rotational
centers in a non-periodic fashion. On the right, we see a chaotic time series
corresponding to the variable x, for
3000 uniformly sampled points from a trajectory computed using the Runge-Kutta
method of order 4 with step size 0.0001.
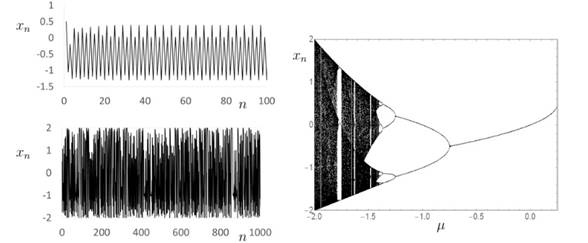
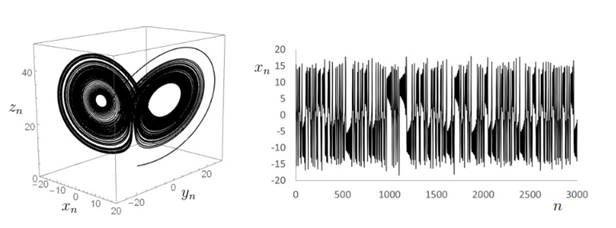
Figure 2. The quadratic family xn+1=xn2+µ presents different dynamical behavior
for different values of the parameter µ.
On the left, we see the time series of a typical orbit for µ=-1.3 (top), and µ =-2
(bottom). On the right, we see the orbit diagram for the quadratic family in
the interval -2≤ µ≤ 0.25, where we
see the long term behavior of typical bounded orbits. The vertical section of
the diagram at µ =-1.3 shows a
period-4 cycle, that corresponds to regular periodic behavior, and at µ =-2 shows chaotic behavior.
Hydrological data
The hydrological time series of
evapotranspiration, precipitation, and stream flow analyzed in this paper come
from the Azul and Tandil regions in the central eastern part of Argentina. See
Figure 3.
The upper creek basin of Del Azul has an
area of 1024 km2, see (Guevara Ochoa et al., 2018), and the altitude of the basin varies between 367 and
129m. The highest part is located in the SE, in the Tandilia system and
presents slopes larger than 6%, see (Poire and Spalletti, 2005). Towards the NW
the basin lies in a lowland region where the slopes are smaller than 1%, see
(Guevara Ochoa et al.,2019).
Figure 4
shows the hydrological time series of evapotranspiration, precipitation, and
stream flows studied in this work. Table 1 presents some basic statistics of
the distribution of values for the sequences including mean, standard
deviation, median, skewness and kurtosis.
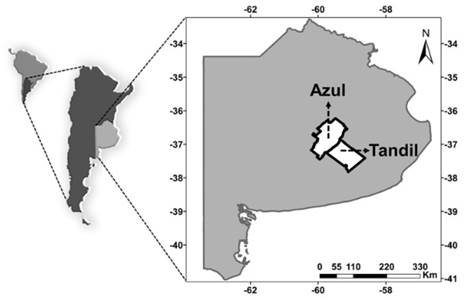
Figure
3. The picture shows, from left to right, the location of Argentina in South
America, the location of the province of Buenos Aires in Argentina, and the
location of Azul and Tandil areas in the province of Buenos Aires, where the
hydrological variables have been measured.
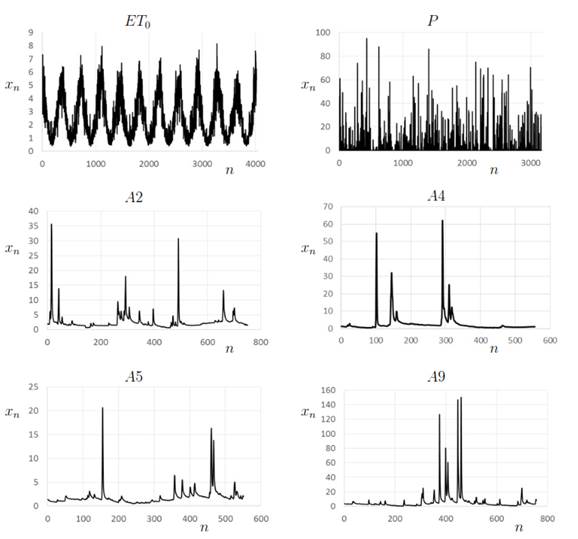
Figure
4. The time series studied in this
work including evapotranspiration (ET0), precipitation (P), and
stream flows (A2, A4, A5, and A9). In these plots the horizontal axis
corresponds to time in units of days.
Table 1. Basic statistical
information about the time series considered in this work. Notice the large
skewness characteristic of precipitation and flow time series.
|
Time series
|
Length
|
Mean
|
Std. Dev.
|
Median
|
Skewness
|
Kurtosis
|
|
Lorenz system
|
3000
|
-0.67
|
7.89
|
-0.98
|
0.15
|
2.35
|
|
Quadratic map with µ = -2
|
3000
|
0.00
|
1.41
|
0.02
|
0.00
|
1.50
|
|
Quadratic map with µ =
-1.3
|
3000
|
-0.51
|
0.73
|
-0.62
|
0.08
|
1.14
|
|
Evapotranspiration
|
4018
|
2.67
|
1.62
|
2.33
|
0.51
|
2.20
|
|
Precipitation
|
3164
|
2.46
|
8.36
|
0.00
|
5.20
|
35.98
|
|
Stream flow A2
|
751
|
2.60
|
2.80
|
1.89
|
6.48
|
60.36
|
|
Stream flow A4
|
556
|
2.76
|
5.33
|
1.44
|
6.55
|
56.74
|
|
Stream flow A5
|
551
|
1.83
|
1.73
|
1.47
|
5.85
|
48.71
|
|
Stream flow A9
|
756
|
5.92
|
11.98
|
3.20
|
7.55
|
75.32
|
Evapotranspiration
Evapotranspiration is the hydrological
variable of greatest relevance in the subhumid-humid Pampas, where about 85% of
the water that precipitates is lost through this process, see (Weinzettel and
Usunoff, 2001; Rivas et al., 2002).
The estimation of the potential evapotranspiration in this area is essential,
since the primary productivity is directly linked to water availability, see (Degano
et al., 2018). The land use in the
Azul basin is mainly rural agricultural and pastures. The highest temperatures
occur during the period from December to March (summer) with a monthly average
of 20°C, and the lowest temperatures occur during the period from June to
August with a monthly average of 8°C.
A time series of evapotranspiration from
the Tandil region is shown in Figure 4 (top left). We can see a seemingly
periodic signal, but the peaks and valleys are not exactly distributed
periodically in time and have different magnitudes.
Evapotranspiration from a vegetated surface
depends on meteorological parameters, crop factors and environmental
conditions. The process is connected to the available energy, whose main source
is the direct solar radiation, and to environmental parameters such as air
temperature. The driving force of this process is the difference in pressure
between the water vapor on the evaporating surface and the water vapor in the
surrounding atmosphere, see (Allen et al.
1998).
The Oficina de Riesgo Agropecuario (Agricultural Risk Office) calculates the Reference
Evapotranspiration ET0 with the FAO (Food and Agricultural
Organization) Penman-Monteith Equation, (Allen et al., 1998), see equation (2). The ET0 is calculated
with in situ biophysical variables provided by the Sistema Meteorológico Nacional of Argentina (SMN), measured at
Tandil station (n° 87645), and the data was subjected to the corresponding
consistency analysis. A hypothetical reference crop with an assumed crop height
of 0.12 m, a fixed surface resistance of 70 s/m, and an albedo of 0.23 were
used. ET0 is reference evapotranspiration in [mm/day], and it is
given by
 (2)
(2)
where Rn is the net radiation at
the crop surface [MJ m-2 day-1],
G is the soil heat flux density [MJ m-2
day-1], T is the mean
daily air temperature at 2m height [°C], µ2
is the wind speed at 2m height [m s-1], es is the saturation vapor pressure [kPa], ea is the actual vapor
pressure [kPa], the difference es-ea is the saturation vapor
pressure deficit [kPa], ∆ is the slope of the vapor pressure curve [kPa °C-1],
γ is the psychrometric constant [kPa °C-1], 0.408 is a conversion
factor to mm/day, 900 is a coefficient for the reference crop [kJ-1
Kg K day-1], 273 is a conversion factor to express the temperature
in Kelvin degrees, and 0.34 is a coefficient resulting from assuming a crop
resistance of 70 s/m and an aerodynamic drag of 208/µ2 for the reference crop [s/m].
The study of Wang et al. (Wang et al., 2014) seems to have been the
first one to address evidence of chaos in an evapotranspiration time series.
They applied the reconstruction method and conducted successful short term
forecast experiments using local approximations obtained based on chaos theory.
Precipitation
For this study we counted with the
pluviometric information from the Azul hydrometeorological station of the SMN.
According to the SMN, the mean annual precipitation is 902 mm. March is the
rainy month with an average precipitation of 120mm, and the months of June and
July are the driest with an average of 45mm.
A time series of precipitation is shown in
Figure 4 (top right). The sequence corresponds to a period of more than 8 years
of measurements. The picture shows values of the daily precipitation in
millimeters from a meteorological station in the Azul basin.
The precipitation time series are currently
being used to reinforce the early alert system of floods in the city of Azul,
see (Cazenave and Vives, 2014), and have been evaluated for several
hydrometeorological studies like, for example, (Venere et al., 2004; Guevara Ochoa et
al., 2017). More information about the Azul region can be found in (Barrucand
et al., 2007).
Several studies of
precipitation time series from the point of view of chaos theory are reviewed
in (Sivakumar, 2017). Precipitation time series are often considered as the
result of a stochastic process. However, this seemingly random behavior may be
due to the response of a deterministic chaotic system.
Stream flow
We consider
four time series of daily Azul stream flows [m3/s] denoted by A2
(751), A4 (556), A5 (551), and A9 (756), see Figure 4 and Table 1. Stream flow
time series show complex behavior with a seemingly periodic base flow and peaks
that corresponds to floods from irregularly distributed precipitation events.
The number of variables that participate in the generation of these time series
is large, but it has been found that in some cases, there are only a few
generalized variables that may be able to model the behavior of the system. The
study of Kedra (2014) is an excellent example of a successful application of
the chaotic approach in a study of river flow. For a review of several studies
of river flow using chaos theory see (Sivakumar-2017).
THE 0-1 TEST FOR CHAOS
The 0-1 test
receives as input a one-dimensional time series xn for n = 1, 2,
..., N. The data is used to drive a
two-dimensional system with components given by
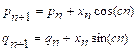 (3)
(3)
where c ϵ (0,2π) is a fixed constant. These
new sequences, given by pn
and qn, represent the
Euclidean extensions of the system to include symmetries under rotations and
translations, see (Bernardini and Litak, 2016). We are interested in the growth
rate of the mean squared displacement of the trajectory (pn, qn)
as a random walk in the plane. The starting point for the walk is set to the
origin, so that p1=q1=0. The time-average mean
squared displacement Mc(n) is given by
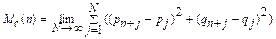
and its growth
rate is defined by
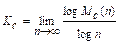
The limits Mc(n) and Kc can
be shown to exist under general conditions, and Kc takes either the value Kc =0 signifying regular dynamics, or the value Kc =1 signifying chaotic
dynamics. This is justified for large classes of dynamical systems, see (Gottwald
and Melbourne, 2016) and references therein. In the regular case (periodic or
quasiperiodic dynamics) the trajectories for the system given by equation (3)
are typically bounded, whereas in the chaotic case the trajectories typically
behave like a two-dimensional Brownian motion with zero drift and hence evolve
diffusively. The diffusive or bounded nature of the trajectories can be seen in
a plot of the walk (pn, qn). A convenient method for
distinguishing these growth rates, bounded or diffusive, is by means of the
mean square displacement Mc(n) which accordingly is either bounded
or grows linearly. The diagnostic parameter Kc
captures this growth rate.
The values of Mc(n) present oscillations that sometimes make the analysis more
difficult, and therefore it is convenient to adjust them before estimating the
growth rate. The oscillations are computed with the following formula,
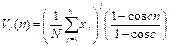 (4)
(4)
Then, the average
displacement is changed from Mc(n) to Dc(n)= Mc(n)- Vc(n). When the oscillations are removed it
is possible for this quantity to become negative. Then, to further set the
estimator we add the term a min Dc(n) with a>1, so that
the new estimator is now denoted by Dc*(n)=
Dc(n)+a min Dc(n). The value
of a=1.1 is used in (Gottwald and
Melbourne, 2016), as in this work.
There are several
methods to measure the growth rate. The correlation method presents some
advantages that have been reviewed recently in (Gottwald and Melbourne-2016),
and is the one used in this work. In order to estimate the growth rate, we
compute the correlation between the vectors ξ
= {1, 2, 3, ..., N}, and D = {Dc*(1),
Dc*(2), Dc*(3), ..., Dc*(N)} using the definition,
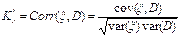 ,
,
where cov and var stand for covariance and variance, respectively. The quantity Kc* measures the
level or strength of the correlation of D
with a linear growth.
The final
diagnostic parameter that provides the output of the test is the number K given by
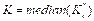 (5)
(5)
where Kc* is computed
for 100 values of c chosen at random
in the interval (π/5, 4π/5). This reduced interval of values of c is used to avoid resonances that can
mislead the interpretation of the results. If K≈0 then the time series is classified as regular (periodic or
quasi-periodic), and if K≈1 then the
time series is classified as chaotic. In practice, the estimated parameter K is found for values of n<<N, and (Gottwald and Melbourne, 2016) recommends the use of N/10, as we do here.
Finally, it is
convenient to plot the values of K as
a function of the length of the series in order to see if there are trends,
especially when it is not completely clear if the time series under analysis
may be long enough to capture the full spectrum of the system dynamics.
In order to illustrate
the application of the test and compare the results, we applied the test to
known chaotic and regular time series from the Lorenz system and the quadratic
map. See Figures 5 and 6.
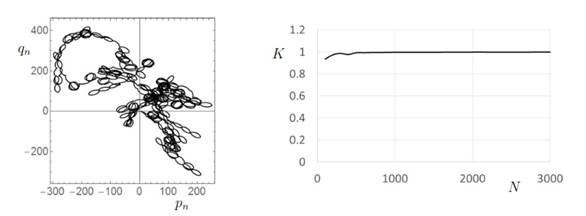
Figure 5. The 0-1 test applied
to the time series of the variable x
of the Lorenz system for the trajectory in Figure 1. On the left, we present a
sample of the random walk of the variables pn
and qn, given by equation
(3), showing diffusive behavior. On the right, we see the parameter K given by equation (4), as a function
of the length N of the time series,
converging to a value of 1, and indicating chaotic motion.
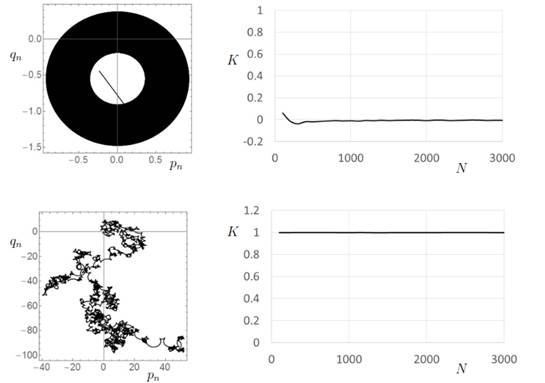
Figure 6. The 0-1 test for
chaos applied to two time series from the quadratic map xn+1=xn+µ. At the top left, we see the random
walk in the pq-plane for the case
with µ =-1.3. The random walk is
bounded. At the top right, we show the parameter K as a function of the length of the sequence, showing convergence
to 0. The test classifies this sequence as regular, as expected. At the bottom
left, we present the pq-plane showing
a diffusive walk for the case µ =-2,
and on the right, we see the parameter K
converging to 1, as we increase the length of the sequence. The test correctly
classifies this sequence as chaotic.
RESULTS
In this section we
present the result of the 0-1 test for chaos, show examples of the behavior of
the two dimensional walk given by the orbits of (pn, qn),
and compute the value of K as a
function of the length of the sequence, for the hydrological time series of
Figure 4.
The values of K for each one of the time series is presented in Table 2, and
except for the regular time series that corresponds to the periodic orbit of
the quadratic function, the values of K
all lie above 0.99. This means that the 0-1 test for chaos classifies the time
series as chaotic.
Table 2. The results of the
0-1 test on the sequences studied in this work. The values of K in the table correspond to the median
of Kc* for 100
values of c selected at random in the
interval (π/5, 4π/5), see equation (5).
|
Time series
|
K
|
|
Lorenz system
|
0.998
|
|
Quadratic map with µ = -2
|
0.998
|
|
Quadratic map with µ =
-1.3
|
-0.006
|
|
Evapotranspiration
|
0.998
|
|
Precipitation
|
0.997
|
|
Stream flow A2
|
0.992
|
|
Stream flow A4
|
0.998
|
|
Stream flow A5
|
0.998
|
|
Stream flow A9
|
0.995
|
Figure 7 shows
the result of the test for the time series of evapotranspiration, precipitation
and stream flow studied in this work. The sample plots of an orbit of (pn, qn) present diffusive behavior. Moreover, in all cases,
the curve of K as a function of the
length of the time series shows convergence of K to 1. Even for the short time series of stream flow it is
possible to see a clear trend in the behavior of K towards 1. We present the results for the sequence A9 that is
representative of the behavior of the four stream flow time series.
DISCUSSION
We have presented the
results of the application of the 0-1 test to several time series. For the
Lorenz system and the quadratic map, the test is able to distinguish regular
from chaotic behavior. For the hydrological time series of evapotranspiration,
precipitation, and stream flow from Argentina, the test classified all the time
series as chaotic. This implies that if we assume that these time series were
generated by deterministic systems, then these systems behave chaotically. The
question in the title refers to the possibility that this result applies to
other hydrological observables. We also notice that with sequences of more than
500 points it is enough to have a clear idea of the convergence of the values
of K.
We presented the
Lorenz system as a prototype of continuous deterministic chaotic dynamics, and
the quadratic equation as a prototype of discrete deterministic chaotic
dynamics. We may ask if any of the systems analyzed in this work may classified
in one of these two types or their several variants, i.e., is there a
deterministic low dimensional nonlinear system of differential equations, like
the Lorenz system, that can provide an accurate description of the dynamics? Is
there a deterministic nonlinear discrete system, like the quadratic map, that
could provide a good model for the description of the behavior of these
variables? We can also ask if a stochastic approach would be more appropriate
for some of them, and if other approaches need to be developed to understand
them.
Nature seems to defy
all kinds of approaches, stochastic, deterministic and chaotic. These different
approaches are applied with the goal of obtaining information about different
aspects of nature. However, due to the nonlinear nature of the phenomena that
interact at a wide range of spatio-temporal scales, the behavior of the
observables is not necessarily well represented by a superposition principle,
where the sum of these characteristics gives as a result the behavior that we
measure. Natural time series are the result of dynamical systems that may
contain at the same time all these characteristics that we can, sometimes, get
to see reflected on the results we obtain with our limited knowledge and tools.
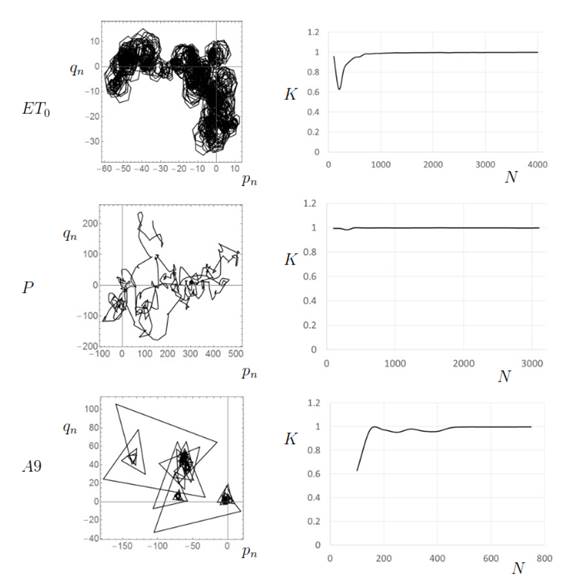
Figure
7. The result of applying the 0-1 test to time series of evapotranspiration
(top), precipitation (center), and stream flow A9 (bottom). On the left, we
present the random walk in the pq-plane
showing diffusive behavior. On the right, we present the graphs of the
parameter K as a function of the
length of the time series. All sequences show convergence of K towards 1.
We stress the point
suggested by the results of this paper: if we assume that the systems under
study are deterministic (which not every researcher is comfortable considering
as a fact), the test performed in this work classifies them as chaotic. This,
in turn, implies the necessity to intensifying the study of chaotic techniques
to better understand these systems in order to perform effective short term
forecasts, since long term forecasts would not be possible. On the other hand,
the historical problem of the availability of complete and long accurate
observations is one of the main reasons that these types of study are so difficult
to perform and apply.
The final answer to
these types of questions remains still open, and may be considered one of the
most difficult and exciting areas of research in contemporary science.
Therefore, we hope that this paper provides an example, raises awareness, and
underlines the use of some of the tools that are being developed and explored
for a better understanding of the behavior of natural phenomena.
The results in this
paper support the idea that finding evidence of chaos and performing a more
detailed study of these variables may be helpful in the understanding of the dynamics of several hydrological
variables, and that a first classification can be made using the 0-1 test for
chaos. The study of other methods including the phase space reconstruction
approach, the possible modeling of the system with local approximations, and
the application of stochastic methods are left for future work.
ACKNOWLEDGEMENTES
We appreciate the Comisión de
Investigaciones Científicas de la Provincia de Buenos Aires (CICPBA) and the
Consejo Nacional de Investigaciones Científicas y Técnicas (CONICET), both of
Argentina, for funding this research. We would like to thank Dr. Guillermo Collazos for providing us with the
sequences of stream flows and for helpful discussions to improve this work. María Florencia Degano acknowledges that this work is part of her
doctoral project Desarrollo e implementación de sistemas automáticos de alerta
de inundaciones y sequias en el área sur de la cuenca del Rio Salado, provincia
de Buenos Aires.} FONARSEC-19/13.
Allen, R. G., Pereira, L. S.,
Raes, D., and Smith, M. (1998). Crop evapotranspiration. Guidelines for
computing crop water requirements. Irrigation
and Drainage Paper No. 56, FAO, Rome, Italy.
Barrucand, M. G., Vargas, W.
M., Rusticucci, M. M. (2007). Dry conditions over Argentina and the related
monthly circulation patterns. Meteorology
and Atmospheric Physics, 98(1-2), 99-114.
Bernardini, D., Litak, G.
(2016). An overview of 0-1 test for chaos. Journal
of the Brazilian Society of Mechanical Sciences and Engineering, 38(5), 1433-1450.
Cazenave, G.,
Vives, L. (2014). Predicción de inundaciones y sistemas de alerta: Avances
usando datos a tiempo real en la cuenca del arroyo del Azul. Revista de Geología Aplicada a la Ingeniería
y al Ambiente, 33, 83-91.
Chowdhury, D. R., Iyengar, A.
N. S., Lahiri, S. (2012). Gottwald Melbourne (0-1) test for chaos in a plasma. Nonlinear Processes in Geophysics,19, 53-56.
Degano, M. F., Rivas, E. E.,
Sanchez, J.M., Carmona, F., and Niclos, R. (2018). Assessment of the Potential
Evapotranspiration MODIS Product Using Ground Measurements in the Pampas. To
appear in Proceedings of the IEEE,
ARGENCON, San Miguel de Tucuman, Tucuman, Argentina, pp. 1-5.
Devaney, R. L. (2003). An Introduction to Chaotic Dynamical Systems.
Cambridge, MA, USA: Second Edition. Westview Press.
Falconer, I., Gottwald, G. A.,
Melbourne, I., and Wormnes, K. (2007). Application of the 0-1 Test for Chaos to
Experimental Data. SIAM Journal of
Applied Dynamical Systems, 6(2), 395-402.
Gottwald, G. A., Melbourne, I.
(2004). A new test for chaos in deterministic systems. Proceedings of the Royal Society of London A, 460, 603-611.
Gottwald, G. A., Melbourne, I.
(2005). Testing for chaos in deterministic systems with noise. Physica D, 212, 100-110.
Gottwald, G. A., Melbourne, I.
(2008). Comment on ``Reliability of the 0-1 test for chaos''. Physical Review E, 77(028201), 1-3.
Gottwald, G. A., Melbourne, I.
(2009a). On the Implementation of the 0-1 Test for Chaos. SIAM Journal of Applied
Dynamical Systems, 8,(1), 129-145.
Gottwald, G. A., Melbourne, I.
(2009b). On the validity of the 0-1 test for chaos. Nonlinearity, 22, 1367-1382.
Gottwald, G. A., Melbourne, I.
(2016) The 0-1 Test for Chaos: A Review. Chapter 7. Skokos, C., Gottwald, G.
A., Laskar, J. (Eds), Chaos Detection and
Predictability, Lecture Notes in Physics, volume (915). Berlin, Germany:
Springer-Verlag.
Guevara
Ochoa, C., Briceño, N., Zimmermann, E., Vives, L., Blanco, M., Cazenave, G.,
Ares, G. (2017). Filling
series of daily precipitation for long periods of time in plain areas. Case
study superior basin of stream del Azul. Geoacta,
42(1), 38-62.
Guevara
Ochoa, C., Lara, B., Vives, L., Zimmermann, E., Gandini, M. (2018). A methodology for the characterization of
land use using medium-resolution spatial images. Revista
Chapingo Serie Ciencias Forestales y del Ambiente, 24(2), 207-218.
Guevara Ochoa, C., Vives, L.,
Zimmermann, E., Masson, I., Fajardo, L., Scioli, C. (2019). Analysis and
correction of digital elevation models for plain areas. Photogrammetric Engineering & Remote Sensing, 85(3), 209-219.
Hu, J., Tung, W., Gao, J., Cao,
Y. (2005). Reliability of the 0-1 test for chaos. Physical Review E, 72(056207), 1-5.
Kantz, H., and Schreiber, T.
(2004). Nonlinear Time Series Analysis.
Cambridge, UK: Second Edition. Cambridge
University Press.
Kedra, M. (2014). Deterministic
chaotic dynamics of Raba River flow (Polish Carpathian Mountains). Journal of Hydrology, 509, 474-503.
Koutsoyiannis, D. (2006). On
the quest for chaotic attractors in hydrological processes. Hydrological Sciences Journal, 51(6),
1065-1091.
Krese, B., Govekar, E. (2012).
Nonlinear analysis of laser droplet generation by means of the 0-1 test for
chaos. Nonlinear Dynamics, 67, 2101-2109.
Krese, B., Govekar, E. (2013).
Analysis of traffic dynamics on a ring road-based transportation network by
means of 0-1 test for chaos and Lyapunov spectrum. Transportation Research Part C, 36, 27-34.
Kriz, R. (2014). Finding Chaos
in Finnish GDP. International Journal of
Automation and Computing, 11(3), 231-240.
Kriz, R., Kratochvil, S.
(2014). Analyses of the Chaotic Behavior of the Electricity Price Series. In
Sanayei, A., Zelinka, I., Rossler, O. E., (Eds.) Interdisciplinary Symposium on Complex Systems, Emergence, Complexity
and Computation, ISCS 2013, 8, 215-226. Heidelberg, Germany: Springer.
Li, X., Gao, G., Hu, T., Ma,
H., Li, T.. (2014). Multiple time scales analysis of runoff series based on the
Chaos Theory. Desalination and Water
Treatment, 52, 2741-2749.
Litak, G., Radons, G.,
Schubert, S. (2009a). Identification of chaos in a regenerative cutting process
by the 0-1 test. Proceedings in Applied
Mathematics and Mechanics, 9, 299-300.
Litak, G., Syta, A.,
Wiercigroch. M. (2009b). Identification of chaos in a cutting process by the
0-1 test. Chaos, Solitons and Fractals,
40, 2095-2101.
Lorenz, E. N. (1963).
Deterministic Nonperiodic Flow. Journal
of the Atmospheric Sciences, 20(2), 130-141.
Lugo-Fernandez, A. (2007). Is
the Loop Current a Chaotic Oscillator? Journal
of Physical Oceanography, 37, 1455-1469.
Melosik, M., Marszalek, W.
(2016). On the 0/1 test for chaos in continuous systems. Bulletin
of the Polish Academy of Sciences, Technical Sciences, 64(3),521-528.
Pasternack, G. B. (1999). Does
the river run wild? Assessing chaos in hydrological systems. Elsevier Advances in Water Resources,
23, 253-260.
Prabin Devi1, S., Singh, S. B.,
Surjalal Sharma, A. (2013). Deterministic dynamics of the magnetosphere:
results of the 0-1 test. Nonlinear
Processes in Geophysics, 20, 11-18.
Poire, D. G., Spalletti, L. A.
(2005). La
cubierta sedimentaria precámbrica/paleozoica inferior del Sistema de Tandilia.
In De Barrio, R. E., Etcheverry, R. O., Caballe, M. F., Llambias, E. (Eds.), Geología y Recursos Minerales de la
provincia de Buenos Aires. Relatorio del XVI Congreso Geológico Argentino,
pp. 51-68.
Rivas, R., Caselles, V., and
Usunoff, E. (2002). Reference evapotranspiration in the Azul River Basin,
Argentina. In Bocanegra, E., Martinez, D., y Massone, H. (Eds.), Actas XXXII AIH & VI ALHSUD Congress of
Groundwater and Human Development, Mar del Plata, Argentina, pp. 693-700.
Schreiber, T. (1999).
Interdisciplinary application of nonlinear time series methods. Physics Reports, 308, 1-64.
Sivakumar, B. (2000). Chaos
theory in hydrology: important issues and interpretations. Elsevier Journal of Hydrology, 227, 1-20.
Sivakumar, B. (2002a). A
phase-space reconstruction approach to prediction of suspended sediment
concentration in rivers. Journal of Hydrology, 258, 149-162.
Sivakumar, B. (2002b). Is
correlation dimension a reliable indicator of low-dimensional chaos in short
hydrological time series? Water Resources
Research, 38(2), 3-1-3-8.
Sivakumar, B. (2004). Chaos
theory in geophysics: past, present and future. Chaos, Solitons and Fractals, 19, 441-462.
Sivakumar, B. (2017). Chaos in Hydrology. Bridging Determinism
and Stochasticity. Dordrecht, Netherlands: Springer Science+Business Media.
Sivakumar, B.,
Jayawardena, A. W. (2002). An investigation of the presence of
low-dimensional chaotic behaviour in the sediment transport phenomenon. Hydrological Sciences Journal, 47(3),
405-416.
Sivakumar, B., Berndtsson, R.
(2005) A multi-variable time series phase-space reconstruction approach to
investigation of chaos in hydrological processes. International Journal of Civil and Environmental Engineering, 1(1),
35-51.
Sivakumar, B., Berndtsson,
R. (Eds.). (2010). Advances in Data-Based Approaches for Hydrologic Modeling and
Forecasting. Singapore, Singapore: World Scientific.
Skokos, C., Gottwald, G. A.,
Laskar, J. (Eds.). (2016). Chaos
Detection and Predictability. Lecture
Notes in Physics, 915. Berlin, Germany: Springer-Verlag.
Tsonis, A. A. (1992). Chaos. From Theory to Applications. New
York, USA: Springer-Science+Business media.
Tsonis, A. A. (2007).
Reconstructing dynamics from observables: the issue of the delay parameter
revisited. International Journal of
Bifurcation and Chaos, 17(12), 4229-4243.
Turcotte, D. L. (1997). Fractals and Chaos in Geology and Geophysics.
New York, USA: Second Edition, Cambridge University Press.
Venere, M.
J., Clausse, A., Dalponte, D., Rinaldi, P., Cazenave, G., Varni, M., Usunoff,
E. (2004). Simulación de Inundaciones en Llanuras. Aplicación a la Cuenca del
Arroyo Santa Catalina-Azul. Mecánica Computacional, 23,1135-1149.
Wang, W., Zou, S., Luo, Z.,
Zhang, W., Chen, D., Kong, J. (2014). Prediction of the Reference
Evapotranspiration Using a Chaotic Approach. The Scientific World Journal, 2014, 1-13.
Weinzettel,
P., Usunoff, E. (2001). Calculo de la recarga mediante aplicación de la
ecuación de D’arcy en la zona no saturada. In Medina, A., Carrera, J. y Vives,
L. (Eds.). Las caras del agua subterránea, serie hidrogeológica y aguas
subterráneas, Tomo I, pp. 225-232.
Xin, B., Li, Y. (2013). 0-1
Test for Chaos in a Fractional Order Financial System with Investment
Incentive. Abstract and Applied Analysis,
2013, 1-10.
Zachilas, L., Psarianos, I. N.
(2012). Examining the Chaotic Behavior in Dynamical Systems by Means of the 0-1
Test. Journal of Applied Mathematics, 2012, 1-14.
Tipo de Publicación: ARTICULO.
Trabajo recibido
el 29/11/2021 y aprobado para su publicación el 24/02/2022.
COMO CITAR
Marotta, S.; Rivas,
R.; Guevara Ochoa, C.; Degano, M.F. (2022). Does determinism imply caos in
hydrological variables?. Cuadernos del
CURIHAM, 28, 1-14. doi: https://doi.org/10.35305/curiham.v28i.174
Este es un
artículo de acceso abierto bajo licencia: CreativeCommons Atribución -No Comercial -Compartir Igual
4.0 Internacional (CC
BY-NC-SA 4.0)
(https://creativecommons.org/licenses/by-nc-sa/4.0/deed.es)

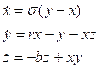 (1)
(1)