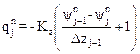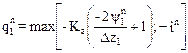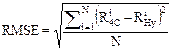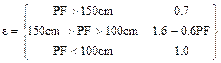ESQUEMA EXPLÍCITO PARA LA SOLUCIÓN NUMÉRICA
DEL FLUJO NO SATURADO EN MEDIOS HETEROGÉNEOS BAJO CONDICIÓN DE NIVELES
FREÁTICOS SOMEROS.
EXPLICIT SCHEME FOR THE NUMERICAL SOLUTION OF
UNSATURATED FLOW IN HETEROGENEOUS MEDIA UNDER SHALLOW WATER TABLE CONDITIONS.
Erik Zimmermann(1) (2)
(1)Consejo Nacional
de Investigaciones Científicas y Técnicas. Buenos Aires, Argentina.
(2)Centro Universitario
Rosario de Investigaciones Hidroambientales (CURIHAM). Facultad de Ciencias
Exactas, Ingenieríay Agrimensura, Universidad Nacional de Rosario. Rosario,
Santa Fe, Argentina
e-mail: erikz@fceia.unr.edu.ar
RESUMEN
Se propone un esquema numérico explícito
de 4 celdas (4C) para la integración de las ecuaciones de flujo en la zona no
saturada diseñado para áreas de llanura con niveles freáticos someros. El
esquema contempla un coeficiente de ponderación para definir la conductividad
hidráulica no saturada representativa entre celdas adyacentes y considera la
heterogeneidad de cada horizonte edáfico. El esquema 4C es comparado con
estimaciones realizadas por el HYDRUS-1D en dos grupos de ensayos modelados,
uno con saturación de superficie durante 10 días y otro con series de
precipitaciones durante 96 días. Los ensayos numéricos se hicieron para 14
tipos de asociaciones de suelos características de la zona de estudio (A° del
Azul, Bs. As.) y 6 profundidades freáticas (entre 300 y 50 cm). Para el primer
ensayo, la respuesta del esquema se considera aceptable con diferencias
porcentuales del orden al 19%. En el segundo, el esquema propuesto estimó
satisfactoriamente las recargas freáticas con diferencias porcentuales del 1%
entre ambos esquemas. Complementariamente, mostró un muy buen ajuste en las
evoluciones de contenidos de humedad de cada estrato. Estos resultados validan
el esquema simplificado propuesto permitiendo una respuesta rápida en términos
de tiempo computacional.
Palabras clave: esquema numérico
explícito, flujo no saturado, llanura, freática somera.
ABSTRACT
An explicit 4-cell (4C) numerical scheme
is proposed for the integration of the flow equations in the unsaturated zone
designed for plain areas with shallow water tables. The scheme contemplates a
weighting coefficient to define the representative unsaturated hydraulic
conductivity between adjacent cells and considers the heterogeneity of each
edaphic horizon. The 4C scheme is compared with estimates made by HYDRUS-1D in
two sets of modeled tests, one with surface saturation for 10 days and the
other with rainfall series for 96 days. The numerical tests were performed for
14 types of soil associations characteristic of the study area (A° del Azul,
Bs. As.) and 6 phreatic depths (between 300 and 50 cm). For the first trial,
the response of the scheme is considered acceptable with percentage differences
of about 19%. In the second, the proposed scheme estimated satisfactorily the
phreatic recharge with percentage differences of 1% between both schemes. In
addition, it showed a very good adjustment in the evolution of moisture
contents of each stratum. These results validate the proposed simplified scheme
allowing a fast response in terms of computational time.
Keywords: explicit scheme,
unsaturated flow, plain, shallow water table.
INTRODUCCION
Los avances de la Hidrología Clásica se
han desarrollado bajo el concepto de cuenca hidrográfica convencional, en el
cual se define claramente un área de aporte, una organización de la red de
drenaje y puede identificarse cada componente de la red con un orden de
jerarquía. Son los denominados Sistemas Hidrológicos Típicos (SHT).
El concepto clásico de cuenca, en sentido
estricto, refleja sólo una parte de los posibles sistemas hidrológicos reales.
La expansión del conocimiento a nivel mundial enfrenta a los hidrólogos con las
grandes llanuras de muy baja pendiente en las cuales no se manifiesta una red
de drenaje lineal o una superficie tributaria, manifestándose transferencias en
sus divisorias, con pluralidad de puntos de salida en algunos casos, y dada la
insuficiente pendiente las respuestas a los estímulos pluviales se dan en
términos de acumulación. Son los denominados Sistemas Hidrológicos No Típicos
(SHN).
La morfología de estos últimos sistemas
condiciona los procesos hidrológicos y el modelo conceptual requerido para
describirlos (Fertonani y Prendes 1983, Kovacs 1983, Tricart 1983, Caamaño
Nelli y Zimmermann 1990, Kruse y Zimmermann 2002). Hay un aspecto clave en el funcionamiento
hidrológico de esos sistemas que es la marcada interacción de la hidrología
superficial con la subterránea.
En función de los niveles freáticos los
excedentes hídricos pueden incorporarse al perfil del suelo o generar derrames
y acumulación superficial de consideración. La zona no saturada (ZNS)
representa la interfaz entre los procesos superficiales y subterráneos, y la
estimación correcta de los flujos de intercambio entre ambos ambientes a través
de ella es crucial a la hora de realizar simulaciones mediante modelos
hidrológicos en áreas de llanura.
Como una alternativa aplicable a estos
sistemas se han desarrollado esquemas de modelación, basados en celdas
interconectadas representativas de los ambientes que intercambian materia,
energía e información. Un ejemplo de esto es el modelo de Simulación Hidrológica
de Áreas de Llanura, SHALL (Zimmermann y Riccardi 2000).
El modelo es hidrodinámico cuasi-3D, que
contempla las componentes subterráneas y superficiales de flujos de agua,
conjuntamente con los flujos verticales hacia el acuífero y la atmósfera. En
cada celda ó unidad de discretización espacial, el modelo SHALL puede
cuantificar dinámicamente variables de estado (almacenamientos por
intercepción, superficial, en el perfil del suelo y subterráneo) y flujos de
intercambio (evapotranspi-ración, ascenso capilar, escurrimiento superficial,
mantiforme y encauzado, a superficie libre y a través de constricciones
-puentes, alcantarillas, sobrepaso de terraplenes, etc.-, infiltración,
percolación profunda y escurrimiento subterráneo).La
aptitud de conectar la hidrología de superficie con la subterránea, lo habilita
para realizar predicciones acerca de evoluciones en los procesos hidrológicos
provocados por acciones antrópicas a escala de cuenca y en el largo plazo.
El modelo ha sido aplicado en sistemas abiertos
del sur santafesino (Zimmermann y Riccardi 2003, Méndez Zacarías y Zimmermann
2011) y sistemas cerrados pampeanos (Zimmermann y Mecca 2010). Actualmente se
prevé la aplicación del modelo en un sector deprimido dela cuenca del arroyo
del Azul, que conforma la vertiente sur del río Salado (provincia de Bs. As.).
Es aquí donde los niveles freáticos se manifiestan someramente otorgando una
particularidad a la modelación de cierta complejidad.
Con fines de adaptación a esta realidad es
que se ha propuesto un esquema numérico novedoso para el flujo de intercambio
superficial-subterráneo para áreas de niveles freáticos someros, el cual se
denominó 4C (cuatro celdas). El esquema propuesto contempla la heterogeneidad
de la ZNS y, a su vez, presenta simplicidad y rápida resolución en términos de
tiempo computacional. Este nuevo esquema numérico se ha incorporado en la
estructura del modelo hidrológico-hidrodinámico SHALL.
Es el propósito de este trabajo comparar
el esquema 4C con estimaciones realizadas por otros modelos de flujo en ZNS de
reconocida trayectoria como el HYDRUS-1D (Simunek et al., 1998) para
ejemplos propuestos y analizar su posible performance en la aplicación del
modelo en las áreas deprimidas del arroyo del Azul.
AREA DE ESTUDIO
La cuenca del arroyo del Azul se ubica en
la zona central de la provincia de Buenos Aires, entre los meridianos 58º 51' y
60º 10' de longitud oeste y paralelos 36º 09' y 37º 19' de latitud sur (Figura
1).
Abarca una superficie de 6237 km² y como
formas destacables se reconocen un sub-ambiente serrano hacia el sur de la
cuenca con altitudes por sobre los 200 msnm (pendiente media del terreno del 5
%), y un sub-ambiente de llanura hacia el norte, por debajo de los 130 msnm
(con pendientes que varían entre 0.5 y 0.8 m/km).
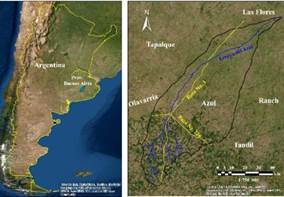
Figura 1. Ubicación relativa de la
cuenca del arroyo del Azul, y principales localidades y vías de comunicación.
Entre ambos ambientes se desarrolla una
zona de transición, caracterizada por suaves ondulaciones.
En el sector más bajo, sumamente llano,
con sus suelos nátricos y drenaje deficiente, se desarrolla principalmente la
cría ganadera extensiva en una matriz de pastizales naturales interrumpida por
las numerosas cubetas y lagunas de carácter mayoritariamente semi-permanente y
por dunas parabólicas y longitudinales (Entraigas et al., 2019).
Desde el punto de vista hidrológico, lo
más notable del comportamiento del agua en cuencas tan deprimidas como la del
Azul es la acumulación del agua sobre la superficie, y la interacción que se
establece entre las aguas superficiales y las subterráneas, conformando un
Sistema Hidrológico No Típico. Específicamente se ha concentrado el interés en
la modelación de un sector del área más deprimida de la cuenca (Figura 2).
El dominio de modelación consiste en un
rectángulo de 24 km en dirección SO-NE y 29 km en dirección NO-SE, el que se
encuentra en su mayor parte incluido en la cuenca superficial del arroyo del
Azul. Para cumplimentar con los fines comparativos es necesario caracterizar
físicamente el medio que constituye la ZNS.
Una característica marcada del área de
estudio es la presencia de niveles freáticos muy someros (50-100 cm de
profundidad) en casi su totalidad, y durante gran parte del año.
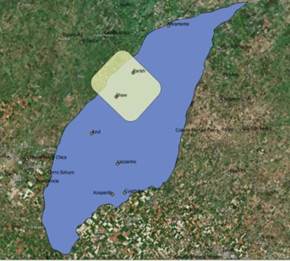
Figura
2. Cuenca del arroyo del Azul y área de interés para la modelación
Estos dos escenarios, características
físicas del medio y presencia de napa somera, marcan las condiciones que deben
respetarse en las simulaciones a comparar.
Caracterización Edafológica
Para este propósito se contó con
información elaborada por el Instituto Nacional de Tecnología Agropecuaria
(INTA) la cual fue cartografiada digitalmente obteniendo un mapa con
asociaciones de perfiles típicos de suelos. En el área de estudio se detectaron
18 series de suelos que se combinan dando lugar a 23 asociaciones, de las
cuales se seleccionaron las más representativas para este estudio. En cada
perfil de las series, en función de su profundidad y su estratigrafía, se detallan
en las cartas de INTA entre 3 y 8 horizontes de los cuales se ha publicado la
composición textural, junto a otros parámetros tales como contenido de materia
orgánica, contenido de carbono, capacidad de intercambio catiónico, pH, etc.Con
esta información, aplicando funciones de pedotransferencia de reconocida
representatividad en la región pampeana (Zimmermann y Basile 2008, 2011, 2014)
se obtuvieron los parámetros hidráulicos respectivos para las series de suelos
en las simulaciones. Los parámetros hidráulicos de la ZNS que se estimaron son
los siguientes: conductividad hidráulica saturada; potencial de entrada de aire
y conectividad de poros para la curva de retención (modelo de Brooks-Corey) y
humedades volumétricas residuales y de saturación. En primer lugar se estimaron
los parámetros medios para cada serie de suelo en toda su profundidad y luego
en función de ellos se valoraron los parámetros para cada asociación ó
consociación de suelos ponderando con la fracción de series de suelos que la
componen (Figura 3).
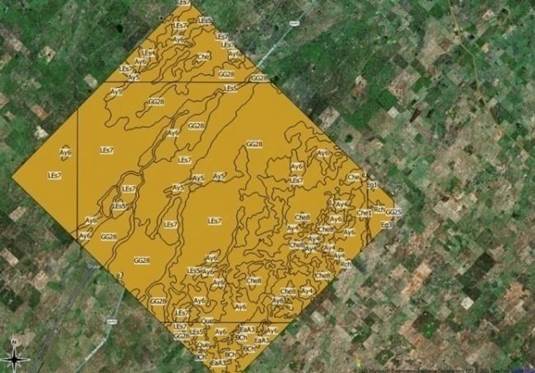
Figura 3. Mapa de ubicación de
asociaciones suelos en el área de estudio
Para estimar humedades características se
emplearon las funciones propuestas por Vereecken et al. (1989), para
densidad aparente la fórmula de Tomasella y Hodnett (1998), para el potencial
de entrada de aire la fórmula de Wösten et al. (1999) y las
conductividades hidráulicas saturadas la fórmula de Saxton et al.
(1986).
En todos los casos se consideró
discriminar los parámetros por horizontesedáficos con el propósito de
caracterizar la heterogeneidad del perfil.
MODELO DE FLUJOS 4C PROPUESTO PARA LA ZONA
NO SATURADA.
El modelo está basado en la ecuación de
Richards, para estimar la redistribución de humedad en la ZNS y los montos de
agua intercambiados con la atmósfera y el acuífero. Solamente está contemplado
el flujo en la dirección vertical. La resolución de la ecuación de continuidad
(ecuación 1) se realiza finalmente en términos del contenido volumétrico de
humedad,è,para conocer una
de las variables del balance hidrológico de manera directa aunque la ecuación
de flujo se plantea en términos del potencial mátrico, ψ, (ecuación
2):
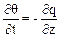 (1)
(1)
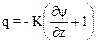 (2)
(2)
donde q es la velocidad de Darcy del flujo
no saturado, è el
contenido volumétrico de humedad, z la coordenada vertical (positiva hacia
arriba), K(θ) la
conductividad hidráulica no saturada, ψ(è) el
potencial mátrico o potencial de succión.
El medio poroso no saturado se representa
en forma discreta mediante un conjunto de 4 celdas que se extienden
verticalmente desde la superficie hasta el nivel freático NF, tres celdas
representativas de cada horizonte edáfico (A,B y C) y la última celda sumergida
en el acuífero freático la cual representa la condición de borde inferior
(Figura4).
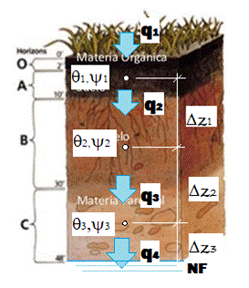
Figura 4. Esquema de discretización
de la ZNS
Los 3 horizontes edáficos están presentes
en la zona de estudio (caracterizada por suelos molisoles). Cada celda
(horizonte) con su contenido de humedad θi,
potencial mátrico ψi y sus
intercambios de flujo qi determinados, separadas por distancias
variables Δzi
según las asociaciones de suelos que las caracterizan. Para la resolución de
las ecuaciones (1) y (2) se ha propuesto un esquema numérico de tipo explícito
en diferencias finitas. El esquema es centrado en el espacio y progresivo en el
tiempo. En los bordes de celdas se evalúan los flujos de intercambio y en los centros
de celdas se estiman las humedades y potenciales:
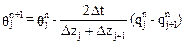 ;
j=1,jf (3)
;
j=1,jf (3)
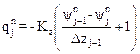 ;
j=2,jf+1 (4)
;
j=2,jf+1 (4)
donde j y n representan los índices de
discretización espacial y temporal, respectivamente, mientras que jf es un
indicador de la celda que alcance el nivel freático. Como valor
“representativo” de la conductividad hidráulica no saturada Kε se
propone aquí:
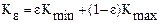 (5)
(5)
donde Kmin
y Kmax son las conductividades hidráulicas no saturadas mínima y
máxima entre los estratos contiguos, respectivamente, y ε un
coeficiente de ponderación (0 <ε< 1). De esta
manera, ε
pondera el peso del estrato menos permeable en el valor del flujo no saturado.
La secuencia de cálculo es la siguiente:
(a) Partir de una condición inicial de humedades è0j en el
perfil, (b) resolver la ecuación de flujo (ecuación 4) para las celdas no saturadas,
(c) resolver la ecuación de continuidad (ecuación 3) determinando las humedades
del perfil en el siguiente paso de tiempo y (d) retomar paso (b) hasta tiempo
de finalización de la simulación.
Para las condiciones de contorno, se
plantea en el borde superior una condición de flujo establecida balanceando la
capacidad de infiltración y la intensidad de precipitación:
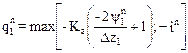 (6)
(6)
donde in es la intensidad de
lluvia efectiva, estimada como la intensidad de precipitación (lámina caída
sobre intervalo de tiempo) que no es interceptada por la vegetación. El primer
término de la ecuación (6) representa la capacidad de infiltración y el segundo
la disponibilidad de agua para infiltrarse.
Como condición de borde inferior se
considera la última celdaincluida en la capa acuífera con humedad de saturación
y potencial mátrico respectivo igual a cero:
 (7)
(7)
Deben conocerse parámetros del suelo tales
como las curvas de conductividad hidráulica K(è), y de retención
de humedad ø(è). En
el presente trabajo se han adoptado las relaciones de Brooks-Corey cuyos
parámetros para cada horizonte y asociación de suelos analizada se han obtenido
mediantes ecuaciones de pedotransferencia, según se ha detallado previamente.
Los lazos de histéresis entre secado y mojadura no se han tenido en cuenta.
Este submodelo de flujos en la ZNS se ha
incorporado en el contexto del modelo de simulación SHALL que se ha descripto
en la introducción.
MODELO DE REFERENCIA HYDRUS-1D
HYDRUS-1D, es un software diseñado
par la simulación del movimiento de solutos, calor y agua en un medio
unidimensional con saturación variable (Simunek et al., 1998). El
programa HYDRUS resuelve numéricamente la ecuación de Richards para el flujo de
agua en medio no saturado y las ecuaciones de tipo convección-dispersión para
el transporte de calor y solutos. Las versión empleada incorpora un término de
sumidero para tener en cuenta la absorción de agua por las raíces de las
plantas, también puede considerar porosidad dual con una fracción del contenido
de agua móvil y fracción inmóvil, aunque en los ejemplos que se analizaron no
se emplearon estos complementos. La región de flujo puede estar compuesta por
suelos heterogéneos o estratificados.
La parte de flujo de agua del modelo puede
tratar con límites prescritos de altura y flujo, límites controlado por las
condiciones atmosféricas, así como por las condiciones de frontera de drenaje
libre. Las ecuaciones de flujo y transporte que gobiernan se resuelven
numéricamente usando elementos finitos lineales tipo Galerkin. HYDRUS también
incluye una optimización de parámetros de reacción y transporte de solutos y/o hidráulicos
del suelo mediante un algoritmo de tipo Marquardt-Levenberg para la estimación
inversa de los mismos.
El programa original se ha complementado
con un menú de interfase gráfica para facilitar la carga de datos e
interpretación de resultados (Simunek et al., 2005). El programa ha sido
ampliamente utilizado en la solución de problemas de flujo y transporte de la
ZNS y constituye un software de referencia mundial.
ENSAYOS REALIZADOS
Descripción general
El objetivo primordial, y sobre el cual se
hará hincapié en las comparaciones, es lograr una satisfactoria estimación de
la percolación acumulada (al final de cada ensayo) del perfil bajo diversas
situaciones en sus contornos. Esto se ve justificado sobre la idea que el
esquema propuesto para el flujo en la ZNS representa la interfase entre
hidrología de superficie y subterránea en el modelo SHALL, por ende es
importante una buena representación de los flujos de intercambios con ambos
ambientes, por encima de una buena representación de la distribución de los
contenidos de humedad en el perfil de suelo.
Además, dado que la composición textural
de los perfiles de suelo tienen un importante contenido de arcilla y los flujos
se preven lentos, se propusieron simulaciones en el largo plazo para contemplar
la llegada desde la superficie al nivel freático.
Las simulaciones sólo se realizaron para
el flujo hidráulico unidimensional, con tres capas represen-tativas de la
heterogeneidad del perfil (horizontes edáficos), sin considerar porosidad dual
ni histérisis en las curvas de conductividad hidráulica y de retención de
humedad.
La condición de borde superior consistió
en flujo establecido para el primer ensayo y una serie de eventos de
precipitación a lo largo de un período de simulación, como condición variable
en el tiempo, en el segundo.
La condición de borde inferior consistió
en un valor de potencial mátrico preestablecido(nulo) a la profundidad
coincidente con el nivel freático adoptado en cada ensayo.
La condición inicial se propuso con el
perfil de humedad en equilibrio, es decir, ψ(z) =-zNF-z,
donde z es la coordenada vertical (z=0 en la superficie y el sentido positivo
del eje z es ascendente).
Para las simulaciones con el modelo
HYDRUS-1D, sediscretizó cada perfil de suelo con intervalos uniformes de 5 cm
para poder analizar el flujo a través de la ZNS, comenzando por el nodo 1 desde
la superficie y avanzando en profundidad hasta la freática.
Se adoptaron los pasos máximos y mínimos
de tiempo sugeridos por el programa para simulación numérica, así como también
para los criterios de iteración y control de paso de tiempo.
Las simulaciones con el esquema de 4
celdas propuesto se hicieron bajo las mismas funciones de curva de retención y
condiciones de borde propuestas para HYDRUS. La discretización del perfil
consistió en hacer coincidir con los baricentros de cada perfil edáfico con los
nodos de simulación de los perfiles de humedad y potencial mátrico, mientras
que el nodo de condición de flujo inferior se seleccionó en función de la
profundidad freática, variable en cada ensayo.
Como el esquema propuesto es de tipo
explícito, se verifica en cada momento de simulación la condición de Courant.
En principio, de las 23 asociaciones de
series de suelos presentes área de estudio, descritas preceden-temente, se
seleccionaron 14 representativas para realizar los ensayos comparativos. Los
diferentes perfiles edáficos se grafican esquematicamente en la Figura 5.
La composición textural general de los
perfiles es franca, con un tercio de cada fracción (arena, limo y arcilla). Los
horizontes A son predominantemente francos-franco arenosos con un 23% de
arcilla, 37 % de limo y 40% de arena en términos medios. Los horizontes B son
predominantemente franco arcillosos, con un 44% de arcilla, 31% de limo y 25%
de arena. En los horizontes C con frecuencia hay presencia de tosca (cementado
con carbonatos).

Figura 5. Esquema de los perfiles de
suelo analizados
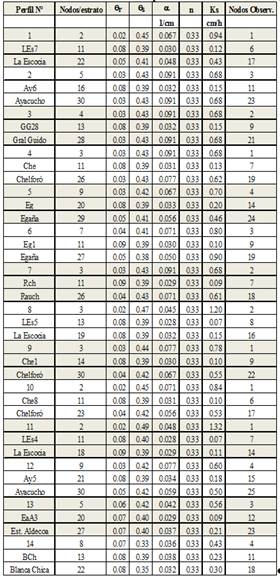
En Tabla 1, se resumen las principales
características de los 14 perfiles edáficos analizados, el símbolo de la
asociación respectiva cuya distribución geográfica se muestra en la Figura 3,
la serie principal del perfil de suelos dominante, el nodo que representa la
profundidad de cada horizonte, las propiedades hidráulicas de cada estrato y
los nodos de observación que coinciden con los baricentros del esquema de 4
cedas simplificado que se propone como alternativa.
Cuantificación de las comparaciones
Para cuantificar el grado de cercania
entre las dos estimaciones de la percolación (HYDRUS y esquema 4C) se
consideraron, a saber: el coeficiente de eficiencia de Nash-Sutcliffe (NSE), el
error medio cuadrático (RMSE), el sesgo (BIAS) y un error porcentual (EP)
definidos bajo las siguientes formulaciones:
 (8)
(8)
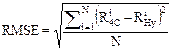 (9)
(9)
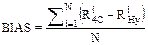 (10)
(10)
 (11)
(11)
donde N es el número de ensayos
realizados, Ri4C y RiHyrepresentan
las recargas acumuladas al nivel freático realizadas con el esquema de 4 celdas
e HYDRUS-1D en el ensayo i, respectivamente y RHymed es
el promedio de recargas acumuladas obtenidas mediante HYDRUS-1D para todos los
ensayos.
Se consideró el coeficiente de ponderación
ε
variable
entre 0 y 1, calculando las recargas R4C para distintos ε
variando con intervalos de 0.05, y evaluando los estadísticos de ajuste para
cada ensayo.
RESULTADOS
Ensayo 1: Intensidad de lluvia constante
durante 10 días
Una primer simulación se propuso con un
flujo de baja intensidad constante de 0.5 mm/h durante 10 dias, como condición
de borde superior, lo que resulta en una superficie casi permanentemente
encharcada.
En el borde inferior se propusieron
diferentes profundidades freáticas, a saber: 2 m, 1.5 m, 1 m y 50 cm, todas
representativas del sector de estudio. No se consideraron profundidades mayores
porque, para el tiempo de simulación propuesto, el flujo no las alcanzaría
dadas las bajas permeabilidades de los estratos iluviales (horizonte B),
principalmente.
Tabla 1. Características de los perfiles
edáficos analizados
La combinación de escenarios entre
condiciones de borde y materiales seleccionados para la simulación resultaron
en 56 casos (N =56), de los cuales en 13 situaciones la solución con HYDRUS-1D
no alcanzó la convergencia y no fueron consideradas en las comparaciones.
Esto ocurrió para los casos de nivel
freático somero (entre 1 m y 50 cm), principalmente. Entre las causas comunes a
este comportamiento, y posibles fuentes de inestabilidades en los casos de no
convergencia, se encontraron: baja conductividad hidráulica del horizonte
iluvial, gran contraste entre conductividades hidráulicas entre horizontes
contiguos y la presencia somera del horizonte iluvial. Posiblemente estos
inconvenientes puedan subsanarse en el HYDRUS mediante una discretización
espacial mas detallada en los contactos entre materiales distintos, pero esto
no fue analizado aquí.
El valor de ε óptimo
que reflejó los mejores NSE y menores errores RMSE y BIAS fue de 1.00. En los
casos de nivel freático más profundo (NF = -2 m) se obtuvieron buenos
resultados también con ε = 0.95.
La Figura 6 resume las concordancias
encontradas con ε = 1, y las diferencias encontradas entre
ambos esquemas. El error porcentual EP en este caso fue del 19%.
Ensayo 2: Período de lluvias de 96 diás.
La intención de este ensayo es analizar el
comportamiento del esquema numérico simplificado bajo situaciones en las que
será aplicado, tanto respecto al sistema hidrológico como a sus forzantes
pluviales. Para construir la serie de lluvias características de la región bajo
estudio se contó con información pluviométrica del período 2014-2018. Se
realizó un estudio estadístico considerando precipitaciones y ocurrencias de
lluvia en intervalos de clase de 96 días. Los resultados obtenidos fueron los
soguientes: precipitación media cada 96 días = 259 mm (desvío estándar = 84 mm)
y ocurrencia media de lluvias cada 96 días = 17 días (desvío estándar = 7
días).
Consecuentemente, se optó por construir
una serie de precipitaciones con 4 períodos de 68 mm caidas en 4 días, separados
entre sí con períodos diferentes, los que fueron seleccionados de manera
arbitraria y no constantes (Figura 7). Esto se realizó con el fin de analizar
el comportamiento de la recarga simulada bajo diferentes condiciones de humedad
previas a cada tormenta.
Con el fin de simplificar el ensayo, se
consideraron sólo 4 de los 14 perfiles edáficos numerados como: 3, 6, 10 y 14
(Figura 5). Los mismos representan situaciones medias y extremas en cuanto a
conductividades hidráulicas y profundidad del horizonte iluvial.
Dado que el tiempo de simulación de este
nuevo ensayo es casi 10 veces el del anterior, se consideraron dos
profundidades adicionales del nivel freático, las cuales se sumaron a los
ensayos: 2.5 m y 3 m.

Figura
6. Concordancia entre ambos esquemas propuestos
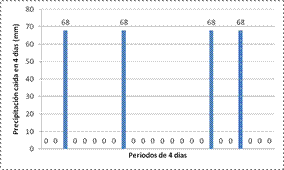
Figura 7. Serie de precipitaciones
construida
Los valores óptimos del coeficientede
ponderación de permeabilidades, ε , fueron diferentes para cada
profundidad del nivel freático, pudiéndose encontrar una correlación lineal
entre ambas variables. Por esta razón se propusieron expresiones para estimar ε en
función de la profundidad freática, a saber:
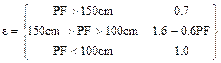 (12)
(12)
donde PF es a profundidad freática.
La Figura 8 resume las concordancias
encontradas encontradas entre ambos esquemas,estimando ε con
las expresiones previas. El error porcentual EP en este caso fue del 1%.
Aún cuando la función objetivo en las
comparaciones ha sido las diferencias entre las recargas acumuladas al final de
cada ensayo, se inspeccionaron las evoluciones de los contenidos volumétricos
de humedad para cada perfil y horizonte edáfico considerado en ambos modelos.
Pudo comprobarse una buena estimación de los perfiles de humedad en el tiempo
por parte del esquema propuesto (Figura 9).
DISCUSION
Se han realizado dos ensayos para testear
un esquema simple, explícito, de resolución numérica basado en diferencias
finitas frente a otro de probada eficacia basado en un esquema de elementos
finitos, de grilla variable, implícito iterativo (HYDRUS-1D) para modelar el
flujo no saturado entre el nivel superficial y el freático.
El sistema a modelar está emplazado en una
zona deprimida de la llanura bonaerense con elevada frecuencia de niveles
freáticos a escasa profundidad.
El esquema simplificado propuesto forma
parte de un modelo de flujo superficial y subterráneo cuasi 3D de celdas
(SHALL) y surge la necesidad de validar su comportamiento en situaciones
similares a las que operará, poniendo enfasis principalmente en el intercambio
de flujo (recarga) entre ZNS y acuífero
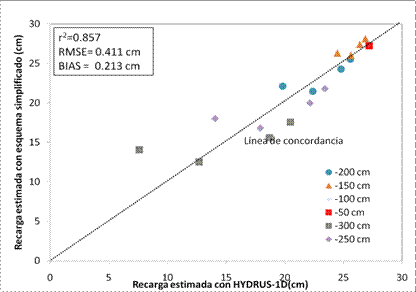
Figura 8. Concordancia entre ambos esquemas propuestos

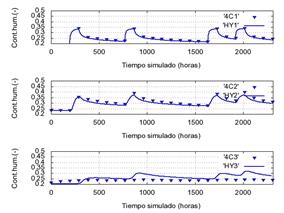
Figura 9. Evolución de contenidos de
humedad en el segundo ensayo para los 3 horizones edáficos del perfil N° 6 y
profundidad de napa -150 cm (izquierda) y perfil N° 10 profundidad de napa -300
cm (derecha). Simulación con HYDRUS-1D (líneas continuas, HY1, HY2, HY3) y
esquema 4C (triángulos, 4C1, 4C2, 4C3).
Se consideran 14 tipos de perfiles
edádicos representativos de la zona, cuyas propiedades hidráulicas se han
obtenido mediante funciones de pedotransferencia.
El primer ensayo propuesto para las
comparaciones, implica una situación difícilmente alcanzada en la realidad, son
10 dias consecutivos de precipitación de baja intensidad, pero ha permitido
conocer los comportamientos de los modelos a comparar en un escenario de saturación
progresiva bajo niveles freáticos de someros a casi superficiales.
El comportamiento del esquema simplificado
fue aceptable (r2 = 0.848, RMSE = 0.328 cm), aunque con una
tendencia a la sobreestimación de la recarga respecto al HYDRUS (BIAS = +1.098
cm).
Cabe mencionar que la propuesta del
coeficiente de ponderación de permeabilidades de horizontes adyacentes tuvo
como efecto darle el peso total al horizonte menos permeable, ya que el valor
óptimo fue prácticamente la unidad (ecuación 5). En otras palabras, el
horizonte iluvial controla el flujo en situaciones de saturación superficial y
niveles freáticos poco profundos.
Si bien este ensayo representa una
situación poco común, diferencias del 20% entre ambos esquemas muestran una
expectativa no alcanzada.
En el segundo ensayo, las condiciones del
borde superior propuestas sí representan situaciones comunes a las que será
sometido el esquema simplificado en el contexto de la modelación con el SHALL.
De hecho, estas condiciones se han extraido de estadísticas de precipitación
relativamente recientes.
Dado que la simulación se extiende a 96
dias, con tiempo suficiente para flujos más penetrantes, se incorporan dos
situaciones adicionales de niveles freáticos más profundos como condiciones
para el borde inferior.
Para estos casos el coeficiente de
ponderación de permeabilidades encontró su valor óptimo en 0.7, lo que implica
una distribución del peso para las permeabilidades entre los estratos
adyacentes, caso que se diferencia del ensayo anterior. Esto da la pauta que
para situaciones donde el nivel freático es más profundo el flujo es comandado
por las características hidráulicas de ambos horizontes adyacentes. Cuando el
nivel freático es más somero, el flujo es comandado por el horizonte menos
permeable, como sucede en el ensayo 1. Esta duali-dad de comportamiento
justifica la propuesta de un coeficiente de ponderación vinculado al nivel
freático, mediante una relación lineal, como se propuso en el ítem anterior.
Esta propuesta mejoró sustancialmente el pronóstico de la recarga para el
esquema simplificado (r2 = 0.857).
En este set de comparaciones los errores
cuadráti-cos medios resultaron semejantes (RMSE = 0.411 cm) y los sesgos muchos
menores (BIAS = +0.213 cm). El error porcentual del 1% respecto al sesgo es
bajo y hace que las comparaciones entre ambos esquemas sean similares.
Contemplando que este segundo ensayo se
ajusta a condiciones reales y factibles para la zona de estudio se considera el
desempeño del esquema simplificado propuesto como satisfactorio.
Además, si bien el objetivo propuesto para
los ajustes era una estimación muy próxima en los valores de recarga final acumulada
entre ambos esquemas, la estimación de las evoluciones de humedades en el
perfil resultó muy similar. No obstante en las simulaciones con niveles
freáticos más profundos(mayores incrementos Δz entre
los últimos estratos en el esquema 4C), como se manifiesta en la Figura 9,
derecha, se observa una distorsión en la estimación razón por la cual deberán
analizarse estas situaciones con más detenimiento.
Estos dos elementos dan la pauta que el
esquema simplificado propuesto para ser integrado en el modelo SHALL es un buen
estimador de variables de estado y los flujos de intercambio en la ZNS.
CONCLUSIONES
Se propone un esquema numérico de
diferencias finitas explícito de 4 celdas, físicamente basado, para representar
el flujo no saturado y heterogéneo entre el nivel superficial y el freático. En
este esquema y para la ecuación de flujo, basada en la ecuación de Richards, se
propone una ponderación entre las conductividades hidráulicas de estratos
adyacentes, que presentan contrastes marcados entre sí. El esquema es comparado
con modelos de reconocida trayectoria como el HYDRUS-1D.
El sistema hidrológico a representar se
emplaza en una zona deprimida de la llanura bonaerense con elevada frecuencia
de niveles freáticos someros y presencia de un estrato arcilloso a poca
profundidad.
Se realizan dos ensayos para testear la
bondad del esquema, uno con intensidad de lluvia constante durante 10 días y
otro con una serie de precipitaciones, estadísticamente representativas de la
climatología local, extendida durante 96 dias. En ambos escenarios se
consideraron las características físicas de los perfiles edáficos de la zona de
estudio y la presencia somera de los niveles freáticos.
El primer ensayo representa un situación
hipotética, difícilmente alcanzada en la realidad, pero ha permitido conocer
las respuestas ante escenarios de saturación progresiva con niveles freáticos
casi superficiales. La respuesta del esquema se considera aceptable con
diferencias porcentuales del orden al 19%.
En el segundo, el cual refleja situaciones
estadísticamente posibles en cuanto a series climáticas, el esquema propuesto
presentó un comportamiento satisfactorio, con diferencias porcentuales del 1%
respecto al modelo HYDRUS-1D. Además, muestra un buen ajuste en las evoluciones
de contenidos de humedad de cada estrato.
Se considera que estos resultados validan
el esquema simplificado propuesto permitiendo una respuesta rápida en términos
de tiempo computacional, haciéndolo apto para su inclusión en el modelo SHALL.
REFERENCIAS BIBLIOGRÁFICAS
Caamaño
Nelli, G. y Zimmermann, E. (1990). Tipología de los Sistemas Hidrológicos
Superficiales. XVI Congreso Nacional Asoc. Arg. Geofis. Y Geod.. Bahía
Blanca. Argentina.
Entraigas,
I., Vercelli, N., Fajardo, L. (2019). Plant communities along preferential
superficial water flow paths across a floodplain landscape. Ecohydrology,
12(6), e2124. https://doi.org/10.1002/eco.2124
Fertonani,
M., y Prendes, H. (1983) Hidrología en áreas de llanura. Aspectos
Conceptuales Teóricos y Metodológicos. Coloquio de Hidrología de Grandes
Llanuras. Olavarría.Argentina.,1, p 119-156.
Kovacs,
G. (1983). General Principles of Flatlands Hydrology.Coloquio de
Hidrología de Grandes Llanuras. Olavarría. Argentina, p 297-357.
Kruse,
E. y Zimmermann, E. (2002). Hidrogeología de grandes llanuras.
Particularidades en la llanura pampeana (Argentina).In: Workshop
publication on Groundwater and Human development(pp. 2025-2038).
Méndez Zacarías J. y
Zimmermann E. (2011). Uso De Sistemas De Información Geográfica Para
Parametrización De Modelos De Simulación Hidrológica En Llanuras.XXIII
Congreso Nacional del Agua y VI Simposio de Recursos Hídricos del Cono Sur.
Resistencia. Argentina.
Saxton,
K., Rawls,W., Romberger,J.,and Papendick R. (1986). Estimating generalized
soil-water characteristics from texture.Geoderma, (102),275 -297.
Simunek,
J., Huang K., y Van Genuchten, M. (1998).The HYDRUS code for simulating
the one dimensional movement of water, heat, and multiple solutes in variably
saturated media. Version 6.0, Research Report No. 144, U.S. Salinity
Laboratory, USDA, ARS, Riverside, California, 164pp.
Simunek,
J., Van Genuchten, M. T., & Sejna, M. (2005). The HYDRUS-1D software
package for simulating the one-dimensional movement of water, heat, and
multiple solutes in variably-saturated media. University of
California-Riverside Research Reports, 3, 1-240.
Tricart,
J. (1983) L'Hydrologie des Grans Plains, Quelques Reflexions Methodologiques.
Coloquio de Hidrología de las grandes Llanuras.Olavarría, Argentina, 2, p
1191-1193.
Tomasella,
J. y Hodnett, M. (1998). Estimating soil water retention characteristics from
limited data in Brazilian Amazonia.Soil science,163(3), 190-202.
Vereecken,
H., J. Maes, J. Feyen, and P. Darius(1989). Estimating the soil moisture
retention characteristic from texture, bulk density, and carbon content. Soil
Science. 148, 389-403.
Wösten,
J, A. Lilly, A. Nemes, and C. Le Bas (1999). Development and use of a database
of hydraulic properties of European soils. Geoderma 90, 69-185.
Zimmermann
E. y Riccardi , G. (2000)Modelo de simulación hidrológica superficial para
áreas de llanura. XIX Congreso Latinoamericano de Hidráulica. Córdoba.
Argentina.
Zimmermann,
E. y Riccardi, G. (2003). Modelo hidrológico superficial y subterráneo
desarrollado para la simulación de sistemas de llanura. 1. Aplicación en el
sistema Ludueña (Santa Fe, Argentina). Boletín Geológico y Minero, 114(2),
147-158.
Zimmermann,
E. y Basile, P. (2008). Uso de funciones de pedotransferencia para la
estimación de parámetros hidráulicos en suelos limosos (llanura Argentina). Boletín
del Instituto Geológico Minero de España, 119(1), 71-80.
Zimmermann
E. y J. Mecca (2010).Aplicación del modelo SHALL en los sistemas
hidrológicos de las lagunas don Tomás y bajo Giuliani (La Pampa, Argentina)
para la evaluación de impactos provocados por efluentes y escurrimientos. I
Congreso Internacional de Hidrología de Llanuras. Azul, Buenos Aires, Argentina
.
Zimmermann,
E. y Basile, P. (2011). Estimación de parámetros hidráulicos en suelos limosos
mediante diferentes funciones de pedotransferencia.Tecnología y ciencias del
agua,2(1), 99-116.
Zimmermann,
E. y Basile, P. (2014). Metodología de agregación para estimar conductividades
hidráulicas en suelos heterogéneos insaturados.Tecnología y ciencias del
agua,5(4), 39-55.
Tipo de Publicación: ARTICULO
Trabajo recibido el 27/10/2021 y aprobado
para su publicación el 29/11/2021.
COMO CITAR
Zimmerman,
E. (2021). Esquema explícito para la solución numérica del flujo no saturado en
medios heterogéneos bajo condición de niveles freáticos someros. Cuadernos del
CURIHAM, 27,47-58. DOI: https://doi.org/10.35305/curiham.v27i.169
Este es un artículo de acceso abierto bajo
licencia: Creative Commons Atribución - No Comercial - Compartir Igual 4.0
Internacional (CC BY-NC-SA 4.0) (https://creativecommons.org/licenses/by-nc-sa/4.0/deed.es)