MODELACIÓN PRELIMINAR DEL FLUJO SUBTERRÁNEO EN UN SECTOR DE LA CUENCA
INFERIOR DEL ARROYO DEL AZUL (BUENOS AIRES, ARGENTINA).
PRELIMINARY GROUNDWATER MODELING OF A LOWER SECTOR OF ARROYO DEL AZUL
BASIN (BUENOS AIRES, ARGENTINA)
Erik Zimmermann(1)(2)(*), Luisa Fajardo(3)(4) e
Ilda Entraigas(3)(4)
(1) Consejo Nacional de Investigaciones Científicas y
Técnicas. Buenos Aires, Argentina.
(2) Centro Universitario Rosario de Investigaciones
Hidroambientales. Facultad de Ciencias Exactas, Ingeniería y Agrimensura.
Universidad Nacional de Rosario. Rosario, Santa Fe, Argentina..
(3) Comisión de Investigaciones Científicas de la Provincia
de Buenos Aires. Buenos Aires, Argentina.
(4) Instituto de Hidrología de Llanuras. Azul, Buenos Aires,
Argentina.
(*)e-mail: erikz@fceia.unr.edu.ar
RESUMEN
Se construyó un modelo de flujo subterráneo, de carácter
distribuido, con entradas y parámetros uniformes para todo el dominio de
modelación. Este abordaje simplificado se realizó con el fin de caracterizar
procesos generales y ajustar el modelo conceptual preliminar en el área de
llanura del arroyo del Azul. Se propusieron metodologías a fin de completar las
series discontinuas de niveles freáticos que fueron utilizados como condición
de borde aguas arriba seleccionando una regresión lineal entre anomalías
diarias de diferencias entre precipitación y evapotranspiración potencial con
un retardo semanal con resultados de ajuste satisfactorios. Se consideraron
como parámetros globales de calibración la transmisividad del acuífero, el
coeficiente de almacenamiento, un coeficiente de recarga, una profundidad
crítica para la evapotranspiración y un coeficiente de forma para la curva
evapotranspiración vs. profundidad freática. Los coeficientes de eficiencia de
Nash-Sutcliffe entre niveles modelados y observados en 6 pozos de control
oscilaron entre 0.58 y 0.72. Tras la calibración, se concluyó que los
parámetros obtenidos permiten una representación satisfactoria de la evolución
de los niveles freáticos en los pozos de observación y de los patrones
espaciales de las isofreáticas. Se pone en evidencia el rol prominente del
proceso de evapotranspiración, el cual impacta directamente en el acuífero,
representando una salida relevante del sistema. En el período de simulación de
43 meses, de características levemente secas, la recarga constituyó el 17 % de
la precipitación, el 87 % de la misma retornó a la atmósfera como evapotranspiración,
y el acuífero abastecería el 12.7 % de la evapotranspiración potencial del
período. Se considera que la modelación simplificada permitió una aceptable
representación del comportamiento del acuífero freático.
Palabras clave: modelación
flujo subterráneo, área de llanura, evaporación freática
ABSTRACT
A distributed groundwater flow model has been
constructed, with aggregated inputs and parameters for the entire modeling
domain. This simplified approach was carried out in order to characterize
general processes and adjust the preliminary conceptual model of the sector.
Methodologies to complete the discontinuous series of water tables, which were
used as the upstream condition, have been proposed. A linear regression between
daily precipitation minus evapotranspiration anomalies with a weekly delay and
water table levels was selected due to its good results. The aquifer
transmissivity, the storage coefficient, a recharge coefficient, a critical
depth for evapotranspiration and a shape coefficient for the evapotranspiration
vs. water table depth curve were considered as global calibration parameters.
The Nash-Sutcliffe efficiency coefficients between modeled and observed levels
in six wells ranged between 0.58 and 0.72. After the calibration, it can be
affirmed that the parameters obtained allow a satisfactory representation of
the evolution of observed groundwater levels and of the spatial patterns of the
iso-phreatic curves. The prominent role of the evapotranspiration process is evident,
which directly impacts in the aquifer, which representing a very relevant
output from the system. In the simulation period of 43 months, with dry
characteristics, the recharge constituted 17% of the precipitation, 87% of it
returned to the atmosphere as evapotranspiration, and the aquifer supplied the
12.7% of the ETo of the period. It was considered that the simplified modeling
allowed an acceptable representation of the water table dynamics.
Keywords: groundwater modeling, flatland area, phreatic evaporation.
INTRODUCCIÓN
Los avances de la Hidrología Clásica se han desarrollado
bajo el concepto de cuenca hidrográfica convencional, en el cual se define
claramente un área de aporte, una organización de la red de drenaje y puede
identificarse cada componente de la red con un orden de jerarquía.
El concepto clásico de cuenca, en sentido estricto,
refleja sólo una parte de los posibles sistemas superficiales reales. La
expansión del conocimiento a nivel mundial enfrenta a los hidrólogos con las
grandes llanuras de muy baja pendiente en las cuales no se manifiesta una red
de drenaje lineal o una superficie tributaria, manifestándose transferencias en
sus divisorias, con pluralidad de puntos de salida en algunos casos, y dada la
insuficiente pendiente las respuestas a los estímulos pluviales se dan en
términos de acumulación. Son los localmente denominados Sistemas Hidrológicos
No Típicos (SHN) (Caamaño Nelli et al., 1979).
La morfología de estos últimos sistemas condiciona los
procesos hidrológicos y el modelo conceptual requerido para describirlos
(Fertonani y Prendes 1983; Kovacs, 1983; Tricart, 1983; Caamaño Nelli y
Zimmermann, 1990). Al respecto, la Hidrología Comparada (Falkenmark y Chapman,
1989) ofrece un encuadre metodológico para el análisis de los sistemas
hidrológicos en general contemplando estas particularidades.
Hay un aspecto clave en el funcionamiento hidrológico de
esos sistemas que es la marcada interacción de la hidrología superficial con la
subterránea. En función de los niveles freáticos los excedentes hídricos pueden
incorporarse al perfil del suelo o generar derrames y acumulación superficial
de consideración.
Por otro lado, el enfoque ecohidrológico, como
mirada interdisciplinaria que relaciona la hidrología con la ecología y los
complejos procesos en el ciclo del agua, ofrece para estos sistemas un desafío
particular debido a las múltiples interacciones hidrológicas entre sus
componentes asociadas con las comunidades vegetales que los habitan.
El presente trabajo se plantea en el marco del análisis
de la conectividad hidrológica del sector de estudio. En su forma más simple,
la conectividad es una descripción del grado de relación o asociación dentro de
un sistema, y corresponde a un conjunto estructurado de relaciones espaciales
y/o temporales entre las diferentes entidades que lo conforman (Kool et al.,
2013). En principio, se distinguen dos tipos de conectividad. La conectividad
estructural hace referencia a la arquitectura y composición de un sistema (Noss
y Cooperrider, 1994), esto es, al tamaño, forma, ubicación y arreglo espacial
de los elementos que lo componen (Calabrese y Fagan, 2004), y también a las
relaciones físicas entre esos elementos (Kadoya, 2009). A su vez, la conectividad
funcional está directamente relacionada con el grado y dirección de los
desplazamientos a través del paisaje (Kadoya, 2009) que describen los lazos
entre los diferentes elementos que lo componen (Calabrese y Fagan, 2004).
Aplicando estos conceptos a la conectividad hidrológica,
se la define entonces como la conexión que se establece entre los elementos de
una cuenca, siendo la conectividad estructural aquella referida a los patrones
espaciales que se establecen en el paisaje (es decir, la distribución de las
unidades ambientales que influyen en los patrones de transferencia del agua y
en las trayectorias de flujo); y la funcional como aquella concerniente a cómo
esos patrones espaciales interactúan con los procesos de la cuenca para
producir escorrentía, conexión entre flujos y, por lo tanto, la transferencia
de agua en la cuenca (Fajardo y Entraigas, 2017).
Como una primera fase de investigación, se propone un
modelo matemático de flujo subterráneo, de estructura no compleja, con el fin
de cuantificar los principales procesos hidrológicos que se verifican en la
zona de estudio propuesta. Los resultados derivados permitieron deducir
elementos conceptuales del funcionamiento hidrológico subterráneo como “sostén”
de los procesos que se dan en superficie. En una etapa futura se contemplarán
las evoluciones de niveles freáticos y flujos con la atmósfera para la búsqueda
de las conectividades con las comunidades vegetales de superficie.
AREA DE ESTUDIO
La cuenca del arroyo del Azul se ubica en la zona central
de la provincia de Buenos Aires, entre los 58º 51' y 60º 10' de longitud oeste
y 36º 09' y 37º 19' de latitud sur (Figura 1). Abarca una superficie de 6237
km² y como formas destacables se reconocen un sub-ambiente serrano hacia el sur
de la cuenca con altitudes por sobre los 200 msnm (pendiente media del terreno
del 5 %), y un sub-ambiente de llanura hacia el norte, por debajo de los 130
msnm (con pendientes que varían entre 0.5 y 0.8 m/km), con una zona de
transición entre ambos, caracterizada por suaves ondulaciones.
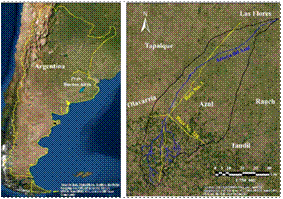
Figura
1. Ubicación relativa de la cuenca del arroyo del Azul, y principales
localidades y vías de comunicación.
En el sector más bajo, sumamente llano, con sus suelos
nátricos y drenaje deficiente, se desarrolla principalmente la cría ganadera
extensiva en una matriz de pastizales naturales interrumpida por las numerosas
cubetas y lagunas de carácter mayoritariamente semi-permanente y por dunas
parabólicas y longitudinales (Entraigas et al., 2019). Desde el punto de vista
hidrológico, lo más notable del comportamiento del agua en cuencas tan
deprimidas como la del Azul es la acumulación del agua sobre la superficie, y
la interacción que se establece entre las aguas superficiales y las
subterráneas, conformando un sistema hidrológico típico de las grandes
llanuras. Específicamente se ha concentrado el interés en la modelación de un
sector del área más deprimida de la cuenca (Figura 2) en el cual se ha
realizado un seguimiento de coberturas vegetales, niveles freáticos, humedades
del perfil y parámetros de suelo.
Antecedentes geológicos y geomorfológicos
Las Sierras de Azul están constituidas por afloramientos
integrados por gneisses y rocas esquistosas precámbricas. En la cuenca del
Azul, estudios de geoeléctrica señalan profundidades del basamento de hasta 120
m en la localidad de Azul y mayores a los 800 m en el área del paraje El
Gualicho (desembocadura de la cuenca del Azul).
En lo que respecta a la composición de la cubierta sedimentaria
del subsuelo dispuesta por encima del basamento, Méndez Escobar et al. (1995)
consignan un acuñamiento de los depósitos del Mar Paranense (Mioceno verde) que
se extiende hasta el norte de la ciudad de Azul, del Mioceno rojo hacia el sur
de la localidad de Shaw (Figura 2), mientras que las arenas puelches se
presentan un poco al norte de Shaw. En el sector superior de la cubierta
consignan un espesor de depósitos que agrupan en la denominada sección
epiparaniana, integrada por depósitos pampeanos y post pampeanos.
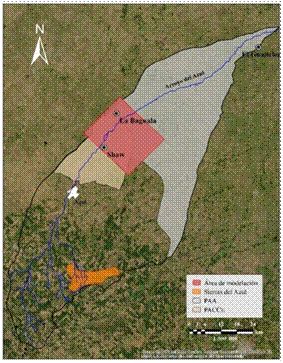
Figura
2. Zona de modelación y sitios referenciados.
Según Zárate y Mehl (2010), el sector bajo estudio se
encuentra en el área extraserrana, comprendido entre las subunidades
geomorfológicas denominadas planicie de agradación con costra calcárea
estratiforme -PACCE- y planicie de agradación aluvial -PAA- (Figura 2). La
PACCE está compuesta por limos castaño rojizos, compactos y carbonatados, con
clastos de costras calcáreas, inmersos en una matriz limosa. Por encima de la
costra calcárea se dispone una cubierta sedimentaria muy somera, de unos
0.50-0.70 m de potencia, muy modificada por pedogénesis. El sustrato
suelo-costra calcárea genera encharcamientos superficiales, así como
condiciones de drenaje interno deficiente en el perfil. El escaso gradiente
generaría condiciones de escurrimiento muy lento. En cuanto a la PAA, está
compuesta por una sección inferior de depósitos limos arenosos,
castaño-rojizos, compactos, con estructuras de corriente y nódulos calcáreos.
Por encima de ésta, se desarrolla una sección superior compuesta por limos
finos gris cenicientos, con estratificación horizontal y eventual geometría
lenticular correspondiente a facies palustres. La PAA funciona en la actualidad
como un ambiente geomorfológico de abanico distal de muy bajo gradiente y
escaso relieve relativo.
Antecedentes hidrogeológicos
El Instituto de Hidrología de Llanuras (IHLLA) dispone de
dos redes de control piezométrico, una freática (6 m) y otra profunda (30 m),
que cubren toda la cuenca del arroyo del Azul. La mayoría de los lugares de
observación consisten en un par de piezómetros, uno de cada red. La superficie
freática se encuentra cerca de la superficie del terreno (2-5 m) en casi toda
la zona. La geometría de la superficie piezométrica a 30 m es similar a la
freática; tanto es así que en el sector central hay varios emplazamientos donde
los niveles piezométricos a 6 y a 30 m no son diferenciables en la práctica
(Zabala et al., 2010).
El IHLLA (2003), en base a la interpretación de ensayos de
bombeo y mediante una modelación matemática de acuíferos, presentó una
estimación de parámetros hidráulicos para la cuenca del Azul (Tabla 1).
Tabla
1. Estimaciones de permeabilidades horizontales (Kh) y verticales (Kv) en la
ciudad de Azul (Varni 2005).
|
Profundidad(m)
|
Permeabilidad
|
Kh(m/d)
|
Kv(m/d)
|
|
0-40
|
Baja
|
5
|
0.5
|
|
40-60
|
Media
|
15
|
8
|
|
60-90
|
Baja
|
10
|
5
|
|
90-120
|
Alta
|
30
|
20
|
Varni (2005) infiere, a partir de la obtención de curvas
de isoprofundidad mediante sondeos eléctricos verticales, que el basamento
cristalino se encontraría entre los 200 m y 450 m en el sector de estudio.
Por otro lado, estima mediante balance de agua, balance
de cloruros y modelación matemática de flujo subterráneo un entorno para la
recarga freática entre el 8 y 15 % de la precipitación.
El mismo autor ajusta mediante calibración valores de
almacenamiento específico entre el 3% y el 5%.
MODELO DE FLUJO SUBTERRÁNEO
El modelo básico de flujo subterráneo consiste en la
resolución numérica de las ecuaciones que gobiernan el movimiento no
estacionario bidimensional (en planta) mediante una aproximación en diferencias
finitas. La ecuación en derivadas parciales se expresa como:
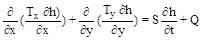 (1)
(1)
donde: Tx es la transmisividad del acuífero en
la dirección x; Ty es la transmisividad del acuífero en la dirección
y; S es el coeficiente de almacenamiento del acuífero; h es la altura
piezométrica; t es el tiempo; x, y son coordenadas espaciales en planta y Q son
funciones de fuente o sumidero expresadas como caudales netos por unidad de
área.
A través de una aproximación en diferencias finitas, lo
que implica reemplazar el continuo del sistema acuífero por un conjunto
equivalente de elementos discretos (celdas), es posible obtener una solución
numérica de la ecuación anterior.
En cada nodo o celda se plantea la ecuación de
continuidad, considerando el almacenamiento de la celda y los flujos de intercambio
con las vecinas y el exterior (Figura 3). Se considera el coeficiente de
almacenamiento por celda, la ley de Darcy para el intercambio de flujos en el
propio acuífero (Q1 a Q4) y las recargas desde la zona no
saturada (Q5) y las extracciones por bombeos y evapotranspiración (Q6).
Las ecuaciones planteadas en cada nodo deben resolverse para las principales
incógnitas, que son los niveles hij. Para la resolución numérica de
la ecuación diferencial se utiliza una forma modificada del método implícito
iterativo de direcciones alternantes proporcionado por Prickett y Lonnquist
(1968) a fin de resolver el conjunto de ecuaciones simultáneas. Esta técnica es
incondicionalmente estable, independientemente del tamaño del incremento de
tiempo.
Las recargas, por su lado, se consideran uniformes para
el área de modelación, y se las define como un porcentaje de la precipitación
mediante un coeficiente ajustable en el período de simulación (b):
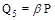 (2)
(2)
Siendo P y Q5 la precipitación y la recarga
diaria, respectivamente.
Para
la evapotranspiración (ET) se consideró un coeficiente reductor (a) de la
evapotranspiración potencial (ETo) como una función exponencial decreciente con
la profundidad de la freática (pf), desde la superficie hasta una
profundidad denominada crítica (pfcrit):
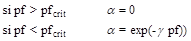 (3)
(3)
Donde g es un parámetro que varía entre 0.4-1.0. Tanto g como pfcrit se consideraron ajustables en las
simulaciones y uniformes en el dominio.
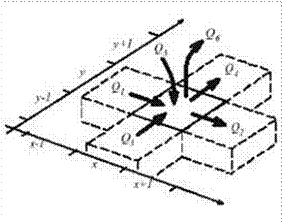
Figura
3. Discretización del dominio de modelación (extraída de Prickett y Lonnquist,
1968)
Para este trabajo se contó con el programa fuente
original de Prickett y Lonnquist, escrito en FORTRAN IV, para acuíferos libres.
El código, fue readaptado para adecuarlo a las condiciones de contorno del caso
de estudio y las ecuaciones propuestas para la recarga y la evapotranspiración
del acuífero.
APLICACIÓN DEL MODELO
Grilla de modelación
El dominio de modelación consistió en un rectángulo de 24
km en sentido SO-NE y 29 km en sentido NO-SE, el que se encuentra casi
totalmente incluido en la cuenca superficial del arroyo del Azul (Figura 2). La
grilla de discretización fue subdividida en elementos cuadrados de 1 km de
lado, totalizando 696 celdas (24 filas, 29 columnas). El período de simulación
del modelo se propuso en función de la información disponible, abarcando desde
octubre de 2014 hasta abril de 2018 (43 meses), con un paso de cálculo temporal
de 1 día.
Condiciones de borde
Las isofreáticas construidas a partir de los registros
obtenidos en 21 pozos de observación ubicados en el área de estudio
manifestaron un patrón de flujo repetitivo (Figura 4), cuya morfología permitió
establecer hipótesis para las condiciones de borde. Este patrón reflejó un
sentido predominante del flujo hacia el noreste, aproximadamente representativo
en la totalidad del área de estudio, coincidente con la orientación de las
márgenes laterales. Por ello las mismas fueron consideradas como líneas de
flujo. El borde oeste del sector está próximo a la divisoria superficial de la
cuenca del Azul, lo que justificaría la imposición de un borde impermeable.
Para el límite este, las isopiezas del patrón de flujo sugieren la definición
de una línea de flujo coincidente con dicho límite.
En los bordes aguas arriba (borde sur) y aguas abajo
(borde norte) se propusieron condiciones de niveles y flujos preestablecidos,
respectivamente (Figura 5). El borde sur cuenta con registros freatimétricos
históricos en numerosos pozos de ese frente. Complementariamente se consideró
la condición de control de flujos regionales hacia el río Salado en el borde
norte.
Los registros históricos de niveles freáticos en el borde
sur fueron discontinuos temporalmente y abarcaron pocas celdas representativas,
por lo que fue necesario diseñar una estrategia de completamiento. Se contó con
datos mensuales de seis pozos cuyos registros contemplaban dos períodos
observados: 10/2014-03/2016 y 04/2017-04/2018.
En principio, se propuso completar los registros de niveles
discontinuos mediante correlaciones con variables ambientales de patrones
análogos, de las que, tras una selección previa, se consideraron las anomalías
acumuladas de las diferencias entre precipitación y evapotranspiración (P-ETo)
y de gravedad. Las anomalías acumuladas de P-ETo, denominadas anomalías
hidrológicas (AH) se construyeron mediante la siguiente ecuación (Zimmermann,
2020):
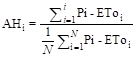 (4)
(4)
Donde: i representa un día de cálculo, N,
el número total de días del período, Pi, la precipitación del
día i; EToi, la evapotranspiración potencial para el
día i.
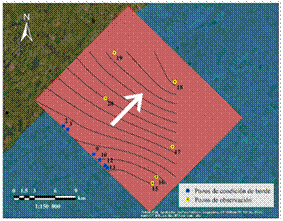
Figura
4. Sentido predominante del escurrimiento subterráneo en el sector modelado.
Las anomalías de gravedad, medidas desde una plataforma
satelital, se refieren a cambios de masa en unidades equivalentes de agua
líquida y fueron publicadas mensualmente en el marco del proyecto GRACE
(Gravity Recovery and Climate Experiment).
En el sector de estudio las profundidades freáticas
oscilan alrededor del metro, lo que pone de manifiesto que la
evapotranspiración es una componente de suma importancia
Se contó con datos diarios de precipitación de dos
sitios, la estación Azul Aero del Servicio Meteorológico Nacional (estación de
confianza) y otra perteneciente a un establecimiento agropecuario cercano a la
localidad de SHAW.
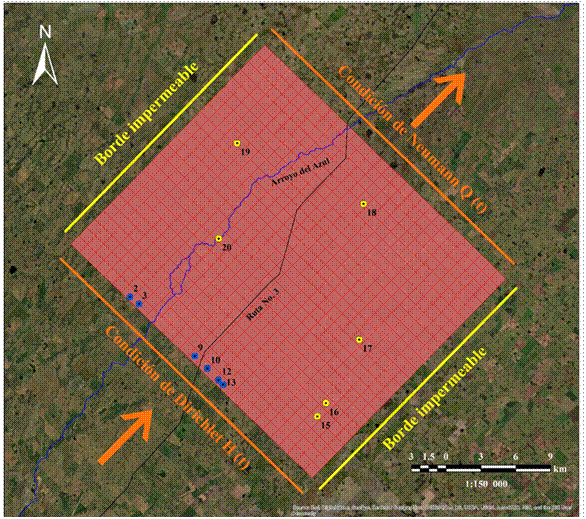
Figura
5. Grilla de modelación propuesta, condiciones de borde seleccionadas y pozos
de observación de niveles freáticos utilizados para construir las condiciones
del borde sur (amarillo) y para control del modelo (azul).
Se dispuso de información de evapotranspiración potencial
estimada mediante el método de Penman-Monteith y con un balance hidrológico
calculado para el área de La Baguala (Varni y Custodio, 2013; Vercelli et al.,
2019), ubicada en el interior del dominio de modelación (Figura 2).
Las anomalías hidrológicas, que fueron calculadas en
forma diaria, se retrasaron entre un dia y una semana para contemplar un
retardo entre el evento superficial y su efecto en los niveles freáticos. Se
obtuvieron las mejores correlaciones con lag de 7 días.
Se optó por considerar las anomalías hidrológicas como
metodología de completamiento temporal de registros freatimétricos por su mejor
correlación (Tabla 2), definición temporal y disponibilidad de información
(Zimmermann, 2020).
Los valores extrapolados temporalmente de los pozos
permitieron completar el período de simulación en los pozos considerados.
Posteriormente, se extrapoló espacialmente esta
información para la totalidad de celdas del borde mediante ecuaciones lineales.
De esta manera pudo completarse la secuencia de datos freatimétricos en cada
celda del borde sur, que fueron considerados como condición de contorno.
Tabla
2. Coeficientes de correlación entre anomalías y niveles freatimétricos de los
pozos considerados.
|
Pozos
|
Anomalías
hidrológicas
|
Anomalías
gravimétricas
|
|
2
|
0.893
|
0.794
|
|
3
|
0.894
|
0.798
|
|
9
|
0.861
|
0.624
|
|
10
|
0.846
|
0.668
|
|
12
|
0.881
|
0.748
|
|
13
|
0.887
|
0.702
|
Para
las condiciones de borde norte, se consideró la condición de flujos regionales
preestablecidos hacia el río Salado. El mismo se ubica a unos 150 km al NE en
cuya dirección el gradiente regional topográfico es de aproximadamente 0.66
m/km (valor estimado a partir de información altimétrica extraída de Google
Earth©). Los caudales efluentes de cada celda se estimaron como
producto entre el ancho (1 km), el espesor freático considerado, la
permeabilidad horizontal de la celda y el gradiente regional estimado hacia el
río Salado.
Geometría estimada del acuífero freático
Según registros estratigráficos, aproximadamente los
primeros 40 m del acuífero freático están constituidos por sedimentos pampeanos
de textura limosa cuyas permeabilidades se muestran en la Tabla 1.
Se consideró, de manera simplificada, un espesor de
acuífero freático de 40 m, consecuentemente con la hipótesis de flujo paralelo
en ese espesor, de acuerdo con las observaciones piezométricas indiferenciadas
entre el acuífero freático y aquellos más profundos (Zabala et al., 2010). Esto
conlleva la suposición que la componente vertical hacia la superficie es
despreciable lo cual, salvo en la descarga de la freática al arroyo del Azul
que sería de carácter local, parece ser una hipótesis razonable.
Condiciones iniciales
Para fijar las condiciones iniciales de la simulación se
consideraron los niveles de las celdas del borde sur en el mes de comienzo de
la simulación, octubre de 2014. Se midieron los gradientes piezométricos en la
dirección del flujo, considerando los niveles de los pozos interiores al dominio
de modelado (15, 16, 17, 18, 19 y 20).
Se extrapolaron los niveles freáticos por celdas,
teniendo en cuenta las cotas del borde sur y las pendientes mencionadas. Se
revisaron las profundidades freáticas considerando cotas de superficie por
celda (extraídas del modelo digital de terreno ajustado).
En casos donde el nivel freático superaba la cota del
terreno, dichos valores fueron corregidos adjudicándoseles un valor mínimo
equivalente a la profundidad radicular de la cobertura vegetal presente en esos
sitios.
CALIBRACIÓN DEL MODELO
Teniendo presente las condiciones de borde, las recargas
y descargas por celdas, conforme a la descripción previa del modelo, se
realizaron las corridas pronosticando la evolución de niveles freáticos por
celda en el período de simulación (octubre 2014-abril 2018, totalizando 1308
días).
Se fijó un período de precalentamiento de 7 meses
(octubre de 2014 - abril de 2015), para los cuales los resultados pueden estar
influenciados por errores en las condiciones iniciales adoptadas. En
consecuencia, el período con resultados confiables se extiende desde mayo de
2015 hasta abril de 2018 (3 años).
Se consideraron como parámetros de calibración la
transmisividad del acuífero, T; el coeficiente de almacenamiento, S; el
coeficiente de recarga, b; la profundidad crítica, pfcrit y el coeficiente de
la curva de evapotranspiración vs. profundidad freática, g.
Para comparar valores calculados por modelación y valores
observados, se contó con los registros freáticos de los seis pozos en el
dominio de modelación desde abril de 2017 hasta finalizar el período de
simulación.
La Tabla 3 detalla los rangos considerados para los
parámetros y los valores de ajuste alcanzados para minimizar las diferencias
entre niveles estimados y observados. La metodología empleada para la
calibración consistió en subdividir el rango de análisis de los parámetros en
sub-intervalos y realizar simulaciones del modelo contemplando todas las
combinaciones de parámetros posibles. Como función objetivo se consideró la
eficiencia de Nash-Sutcliffe (NSE) entre los niveles simulados y observados en
los 6 pozos internos del dominio para los períodos en los cuales se contaba con
registros.
Tabla
3. Rango considerado de variación de
parámetros
y valores ajustados.
|
Parámetro
|
Rango evaluado
|
Valor calibrado
|
|
T (m2/d)
|
100-2000
|
200
|
|
S (-)
|
0.03-0.10
|
0.03
|
|
b (-)
|
0.05-0.5
|
0.17
|
|
Pfcrit (m)
|
0.3-3.0
|
3.3
|
|
g (-)
|
0.4-1.0
|
1.0
|
RESULTADOS ALCANZADOS
Como se observa en la Tabla 3, los parámetros calibrados
guardan mucha similitud con los hallados previamente por otros autores (IHLLA,
2003; Varni, 2005), lo que otorga una mayor certidumbre a los resultados.
La Figura 6 muestra la comparación de los registros
freáticos calculados (líneas continuas) y observados (triángulos invertidos)
para los parámetros calibrados en los 6 pozos de observación.
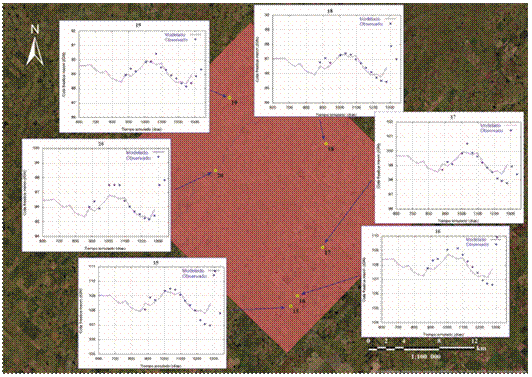
Figura
6. Evolución temporal de los niveles freáticos calculados por modelación
(líneas continuas) y observados (triángulos invertidos) en los freatímetros
seleccionados.
La Tabla 4 muestra los coeficientes de eficiencia de
Nash-Sutcliffe (NSE) para cada caso, donde se aprecia que el modelo refleja
aceptablemente los niveles freáticos observados en la mayor parte de los pozos
de control.
Tabla
4. Coeficientes de eficiencia de Nash-Sutcliffe (NSE) entre los niveles
freáticos modelados y observados.
|
Pozos
de observación
|
NSE
|
|
15
|
0.5822
|
|
16
|
0.6929
|
|
17
|
0.6319
|
|
18
|
0.6480
|
|
19
|
0.7205
|
|
20
|
0.6876
|
Otro aspecto considerado fue el análisis del patrón
espacial de las curvas isofreáticas, el cual resultó muy similar al observado
en el prototipo (Figura 7), y se repite en otros mapas de isofreáticas
calculados por el modelo.
El período de simulación descontado el precalentamiento
abarcó un total de 1096 días (36 meses, comprendidos entre mayo de 2015 y abril
2018). De acuerdo con los guarismos del balance medio del área (Tabla 5), se
deduce que el mismo coincide con un período de características levemente secas,
y esto debe tenerse en cuenta en el análisis. En cuanto a la relación entre la
ET y la recarga del acuífero, la misma es del 87%, es decir que ese porcentaje
de la recarga retorna a la atmósfera como evapotranspiración en el período
analizado.
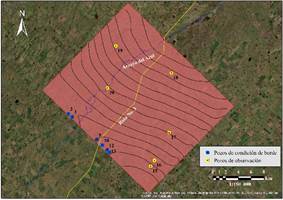
Figura
7. Curvas isofreáticas modeladas (abril de 2018).
Por último, a partir del análisis de la relación entre la
evapotranspiración potencial y la estimada en la modelación, se desprende que
el acuífero freático aporta el 12.7% de la ETo.
Tabla
5. Balance medio areal.
|
|
Precipitación
|
Recarga
|
ETo
|
ET modelada
|
|
|
mm
|
mm
|
mm
|
mm
|
|
Período 2015/18
|
2648.7
|
450.3
|
3071.5
|
389.6
|
|
Promedio anual
|
882.9
|
150.1
|
1023.8
|
129.9
|
Con la información obtenida de la evolución de los
niveles freáticos para cada celda de la modelación, se proyecta analizar sus
estadísticos, permanencias y frecuencias a lo largo del periodo de simulación.
Se cree que esta información, deducida de los resultados del modelo, permitirá
inferir conexiones entre la freatimetría y las coberturas vegetales de
superficie para un amplio sector de la Pampa Deprimida.
CONCLUSIONES
Se construyó un modelo de flujo subterráneo, de carácter
distribuido, con entradas y parámetros uniformes para todo el dominio de
modelación. Este abordaje simplificado se realizó con el fin de caracterizar
procesos generales y ajustar el modelo conceptual preliminar del sector.
Tras una calibración puede afirmarse que los parámetros
obtenidos permiten una representación satisfactoria de la evolución de los
niveles freáticos en los pozos de observación, como así también de los patrones
espaciales de las isofreáticas.
Se pone en evidencia el rol prominente del proceso de
evapotranspiración, el cual impacta directamente en el acuífero, representando
una salida significativa del sistema.
Estos argumentos permiten considerar que la modelación
simplificada permitió una aceptable representación del acuífero freático.
REFERENCIAS
Caamaño Nelli, G. E. y Zimmermann, E. (1990). Tipología de los Sistemas
Hidrológicos Superficiales. XVI Reunión Científica de la Asociación Argentina
de Geofísicos y Geodestas. Bahía Blanca. Argentina.
Caamaño Nelli, G. E., Fertonani, M. E., Prendes, H. H. y Quinodoz, H. A.
(1979) Analysis of Non-Typical Hydrological Systems. Theorical Bases and
Methodology Criteria. Departamento de Hidrología General y Aplicada. Facultad
de Ingeniería en Ciencias Hídricas. UNL. Santa Fe.
Calabrese, J. M. y Fagan, W. F. (2004). A comparison-shopper’s guide to connectivity metrics. Frontiers
Ecology and the Environment, 2(10):529–536.
Entraigas, I., Vercelli, N. y Fajardo, L. (2019). Plant
communities along preferential superficial water flow paths across a floodplain
landscape. Ecohydrology, 12(6):
e2124. https://doi.org/10.1002/eco.2124
Fajardo, L. y Entraigas, I. (2017). Conectividad hidrológica en un
sistema hidrológico no típico. Caso del sector llano de la cuenca del Arroyo
del Azul. Informe de avance beca doctoral CIC.
Falkenmark, M., y Chapman, T. (1989). Comparati-ve
hydrology: An ecological approach to land and water resources. Unesco.
Fertonani, M., y Prendes, H. (1983) Hidrología en áreas de llanura.
Aspectos Conceptuales Teóricos y Metodológicos. Hidrología de Grandes Llanuras.
Olavarría.Argentina. 1, p 119-156.
IHLLA. (2003). Sistema de soporte para la gestión eficiente de los
recursos hídricos en la llanura bonaerense. Inédito, p 267.
Kadoya, T. (2009). Assessing functional con-nectivity
using empirical data. Population Ecology, 51(1): 5–15.
Kool, J. T., Moilanen, A. y Treml, E. A. (2013).
Population connectivity: recent advances and new perspectives. Landscape
Ecology, 28(2): 165-185.
Kovacs, G. (1983). General Principles of Flat-lands
hydrology. Hidrología de Grandes Llanuras. Olavarría. Argentina,
297-357.
Méndez Escobar, R., Usunoff, E. y Weinzettel, P. A. (1995). Aportes al
conocimiento del subsuelo de la cuenca del arroyo Azul (provincia de Buenos
Aires). V Jornadas Pampeanas de Ciencias Naturales. Santa Rosa, La Pampa. Tomo
II, 55-60
Noss, R. F., y Cooperrider, A. Y. (1994). Saving nature’s Legacy:
Protecting and restoring biodiversity. Island Press, Washington, DC, p 416.
Prickett, T. A., y Lonnquist, G. G. (1968). Aquifer
simulation program listing using alternating direction implicit method.
Illinois State Water Survey mimeographed report presented at International
Association of Scientific Hydrology Symposium on Use of Computers in Hydrology,
Tucson, Arizona.
Tricart, J. (1983) L'Hydrologie des Grans Plains, Quelques Reflexions
Methodologiques. Hidrología de las grandes Llanuras. Olavarría, Argentina, 2, p
1191-1193.
Varni, M. (2005). Evaluación de la recarga al acuífero del Azul: Valores
medios y variaciones temporal y espacial. (Tesis doctoral). Facultad de
Ciencias Exactas, Ingeniería y Agrimensura. UNR.
Varni, M., y Custodio, E. (2013). Evaluación de la recarga al acuífero
del Azul: 1. Análisis de las características climáticas. En VIII Congreso
Hidrogeológico Argentino y VI Seminario Hispano Latinoamericano sobre temas
actuales de hidrología subterránea, La Plata. Argentina. doi:
10.13140/2.1.4000.2560.
Vercelli, N., Varni, M., Lara, B., Entraigas, I. y Ares, G. (2019). Linking soil water balance with flood spatial arrangement
in an extremely flat landscape. Hydrological
Processes, 34 (1): 21-32. doi: 10.1002/hyp.13567.
Zabala, M. E., Manzano, M., y Vives, L. (2010). Estudio preliminar del
origen del fondo químico natural de las aguas subterráneas en la cuenca del
arroyo del Azul. Hacia la gestión integral de los recursos hídricos en zonas de
llanura. Volume IM, Varni, I. Entraigas y L. Vives (Eds), 249-256.Azul, Buenos
Aires, Argentina.
Zárate, M., y Mehl, A. (2010). Geología y geomorfología de la cuenca del
arroyo del Azul, provincia de Buenos Aires. Argentina. Hacia la gestión
integral de los recursos hídricos en zonas de llanura, 1, 65-78.
Zimmermann, E. (2020) Completamiento de series temporales de niveles
freáticos en un área deprimida de la llanura bonaerense. Cuadernos del
CURIHAM. 26:55-61. doi: 10.35305/curiham.v26i0.148
REGISTRO BIBLIOGRÁFICO
Zimmermann, E.; Fajardo, L. y Entraigas, I. (2020). Modelación
preliminar del flujo subterráneo en un sector de la cuenca inferior del arroyo
del Azul (Buenos Aires, Argentina). Cuadernos del CURIHAM. 26: 21-30. doi:
10.35305/curiham.v26i0.154
Tipo de Publicación: ARTICULO.
Trabajo recibido el 03/10/2020 y
aprobado para su publicación el 18/11/2020.


![]() (1)
(1)![]() (2)
(2)![]() (3)
(3)
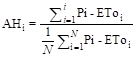 (4)
(4)


