INTRODUCCIÓN
El escurrimiento y su transporte de sedimentos,
nutrientes y plaguicidas, es el principal factor que contribuye a la
contaminación no puntual, afectando negativamente la calidad de los cuerpos de
agua superficiales (Ficklin y Zhang, 2013). La escorrentía es frecuentemente
estimada a partir de la utilización del método de la curva número (CN)
(USDA-NRCS, 2010), o por modelos hidrológicos que presentan alguna ecuación de
infiltración, como la de Green y Ampt (Green y Ampt, 1911).
La CN es un modelo conceptualmente simple, basado en
relaciones empíricas entre la precipitación, el uso de la tierra, el tipo de
suelo y su humedad, que no considera la intensidad de la lluvia ni su duración.
Contrariamente, la ecuación de Green y Ampt es un modelo de infiltración con
base física, que requiere mayor detalle respecto a la dinámica temporal de la
precipitación. A su vez, la CN asume una abstracción inicial previa al
escurrimiento, mientras que con Green y Ampt se modela la escorrentía a partir
de que la intensidad de la precipitación supera la tasa de infiltración
(Ficklin y Zhang, 2013). La ventaja del uso de esta ecuación, es que toma en
cuenta la evolución del proceso de infiltración a partir de procesos físicos
que ocurren en el suelo, por lo que podría estimar mejor el impacto del cambio
de uso de la tierra sobre la escorrentía (King et al., 1999).
La ecuación de infiltración de Green y Ampt es una de
las más usadas en modelos hidrológicos y de erosión (Van den Putte et al.,
2013; Mao et al., 2016). Su incorporación en los modelos CREAMS (Knisel, 1980),
SWMM (Huber y Dickinson, 1988), SWAT (Arnold et al., 1998) y WEPP (Lane y
Nearing, 1989; Laflen et al., 1997) sugiere su versatilidad (Risse et al.,
1995a; Van den Putte et al., 2013). La misma presenta dos parámetros: la
conductividad hidráulica efectiva (Ke) y el potencial mátrico efectivo (Ψ),
respondiendo este último al contenido de agua inicial del suelo y a la tensión
mátrica en el frente de humedecimiento. Se ha observado que los resultados de infiltración
estimados, son sensibles a los cambios en los valores de estos parámetros,
especialmente respecto a Ke (Nearing et al., 1990; De Roo y Jetten, 1999).
Estudios previos realizados con el modelo WEPP (Van der Sweep, 1992; Risse,
1994), mostraron que es necesario un valor realista de Ke para obtener
resultados de escorrentía representativos. Sin embargo, para un variado rango
de suelos, los valores de Ke publicados son poco confiables, de la misma manera
que está poco documentado el efecto del uso de la tierra sobre dicho parámetro
(Nearing et al., 1996).
Para predecir el escurrimiento generado por 330
tormentas en 17 cuencas pequeñas, Rawls y Brakensiek (1986) usaron para estimar
Ke el método desarrollado por estos mismos investigadores (Rawls y Brakensiek,
1983), logrando resultados aceptables. Sin embargo, Darder et al. (2018), al
comparar los resultados de Ke estimados por este procedimiento con los
calibrados a partir de ensayos de infiltración realizados en la región
Pampeana, comprobaron que dicha metodología era poco efectiva.
La CN es un método ampliamente aceptado para predecir
la escorrentía, pudiendo ser su valor utilizado como variable de estimación de
la Ke (Risse et al., 1995a). En este sentido, se han realizado algunos
esfuerzos para encontrar una vinculación entre ambos parámetros (Risse et al.,
1995a; Zhang et al., 1995; Nearing et al., 1996). Nearing et al. (1996)
desarrolló una serie de procedimientos para estimar Ke tomando en cuenta el
grupo hidrológico de los suelos, su contenido de arena y el valor de CN. Estos
autores demostraron utilizando esta forma de estimación de Ke, que la
predicción del volumen de escurrimiento era más realista que el solo uso de la
CN.
El objetivo del presente trabajo fue: analizar la
relación entre Ke y CN, parámetros calibrados a partir de ensayos de
infiltración realizados a campo en pequeñas parcelas y en distintos ambientes
de la cuenca alta del Arroyo Pergamino, determinando a su vez el efecto del
cambio de escala espacial sobre dicho comportamiento.
MATERIALES Y MÉTODOS
Área de estudio y determinaciones
realizadas
El trabajo se realizó con resultados provenientes de
ensayos de infiltración efectuados a campo mediante un simulador de lluvia.
Estas determinaciones se hicieron sobre suelos con aptitud agrícola y ganadera,
en distintos ambientes correspondientes a la cuenca alta del Arroyo Pergamino
(Pcia. de Bs. As.). El clima regional es templado, con temperaturas medias
diarias que oscilan entre los 10 y 12 ºC en el invierno y 23º y 25 ºC en el
verano. La precipitación media anual histórica es de 984 mm (período 1910-2015)
(Estación meteorológica EEA Pergamino, INTA). En las posiciones altas del
paisaje predominan Argiudoles típicos (Serie Pergamino) y sus fases con
distinto grado de erosión, mientras que en los bajos los suelos forman
asociaciones y complejos muy heterogéneos, que contienen proporciones variables
de los suelos encontrados en las tierras altas, entremezclados con Alfisoles
salinos y alcalinos (INTA, 1972).
En los ambientes ganaderos se trabajó en distintos
lotes y a tres distancias respecto del curso de agua principal: 6 m, 30 m y 100
m, presuponiendo la presencia de suelos con características distintas al estar
dispuestos más lejos del arroyo. En los ambientes agrícolas se seleccionaron
lotes bajo siembra directa ubicados en la loma y media loma, con dos sucesiones
de cultivo contrastantes: predominando en algunos casos el cultivo de soja,
mientras que en otros el esquema de rotación estuvo más equilibrado con
gramíneas.
El simulador de lluvia utilizado posee una parcela de
escurrimiento de 50 cm de lado (Irurtia y Mon, 1994). Se hicieron tres
repeticiones por lote y por distancia al curso de agua, aplicando dos
intensidades de lluvia: 60 mm.h-1 y 30 mm.h-1, en el
primer caso durante una hora y en el segundo en un lapso de dos horas. En todos
los casos se determinó la tasa de infiltración cada 5 minutos. No se eliminaron
de la superficie del suelo los rastrojos remanentes del cultivo anterior, ni el
tapiz vegetal en aquellos ambientes bajo pastura. Las simulaciones de lluvia
con una intensidad de 60 mm.h-1 fueron realizadas en mayo de 2011,
siendo en total 85 (28 en lomas, 28 en medias lomas y 29 en ambientes con
aptitud ganadera). En mayo de 2013 se hicieron 74 simulaciones a 30 mm.h-1
(27 en lomas, 27 en medias lomas y 20 en las posiciones bajas del
paisaje). En cada ensayo se tomaron muestras para la determinación de la
humedad gravimétrica edáfica inicial y la porosidad del suelo superficial. Para
mayor detalle de la parte metodológica ver Darder et al. (2018).
Análisis de los resultados generados con
simulador de lluvia
Con los resultados de la lámina total de escurrimiento
y de lluvia de cada ensayo realizado a campo, se estimó primeramente el valor
de S (retención potencial máxima al comienzo de la tormenta), aplicando la
ecuación 1 (Yoo et al., 1993):
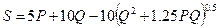 (1)
(1)
Siendo: P = lámina de lluvia (mm); Q = lámina de
escurrimiento (mm).
Posteriormente, los valores de S fueron transformados
a CN mediante la ecuación 2 (Hawkins, 1993):
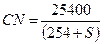 (2)
(2)
El método de la CN fue desarrollado por el Servicio de
Conservación de Suelos de Estados Unidos (USDA-NRCS, 2010) para predecir el
escurrimiento en superficies que oscilan entre 0.0971 y 18600 ha. No obstante,
en el presente trabajo se empleó una superficie menor con la finalidad de
analizar fundamentalmente la relación CN-Ke, observando posteriormente su
comportamiento en una mayor superficie.
A partir de los resultados de tasa de infiltración de
cada ensayo de simulación de lluvia, obtenida cada cinco minutos durante una o
dos horas, se calibró la conductividad hidráulica efectiva y la tensión mátrica
en el frente de humedecimiento, correspondientes al modelo de infiltración de
Green Ampt (Green y Ampt, 1911). Se determinó el grado de vinculación entre
ambos parámetros (CN y Ke) para la escala de los ensayos realizados a campo.
Posteriormente se analizó el grado de ajuste entre los resultados calibrados de
Ke y los estimados mediante la ecuación desarrollada por Nearing et al. (1996)
para suelos bajo agricultura, la cual relaciona la Ke con CN según se detalla
en la ecuación 3:
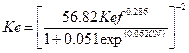 (3)
(3)
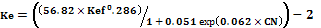
Siendo: Ke = Conductividad hidráulica efectiva; Kef =
conductividad hidráulica efectiva obtenida por tablas para una condición de
barbecho; CN = valor de la curva número calibrada para las condiciones de cada
ensayo.
Utilización del modelo Hec Hms 4.0 (2010)
Mediante el modelo hidrológico Hec Hms 4.0 (2010),
se analizó si la lámina de escurrimiento estimada con los valores de Ke
y CN calibrados con los ensayos de infiltración realizados a campo, se
modificaba con la escala. Para ello, se ejecutó dicho modelo utilizando la
mitad de los resultados de Ke y CN obtenidos según lo detallado en el punto
anterior, bajo iguales condiciones iniciales pero para una superficie de 2 ha.
Se contempló que los valores de estos parámetros, abarcaran el rango de resultados
obtenidos a campo. Posteriormente se comparó la lámina de escurrimiento
generada para las dos escalas (0.25 m2 y 2 ha), según los dos
parámetros calibrados (Ke y CN) y las dos intensidades de lluvia utilizadas.
También se analizó si la relación Ke-CN obtenida con
los ensayos de campo para las dos intensidades de lluvia, se mantenía con el
cambio de superficie evaluada. De esta manera y con la utilización del modelo
Hec Hms 4.0 (2010), se calibraron nuevamente los parámetros Ke y CN
(calibración condicionada) para un área de 2 ha. Para ello se tomó en cuenta la
información inicial de campo: humedad edáfica superficial inicial, hietograma
de lluvia, caudal generado cada 5 minutos para la superficie de 2 ha (calculado
a partir de los milímetros de escurrimiento obtenidos en la parcela del
simulador de lluvia, convertidos a caudal considerando la mayor superficie),
tensión mátrica en el frente de humedecimiento calibrada para los ensayos de
simulación de lluvia, porosidad total del suelo y su contenido de agua bajo
suelo saturado (Darder et al., 2018). Con el mismo objetivo pero sin contemplar
los resultados de caudal determinados con el simulador de lluvia, se realizó
una nueva calibración de Ke (calibración no condicionada), a partir de los
caudales estimados con el modelo Hec Hms 4.0 para distintos valores de CN. En
este caso, se consideró un rango de valores de CN similar al obtenido en las
pequeñas parcelas, aparte de tomar en cuenta el resto de las condiciones
iniciales de los ensayos realizados a campo.
El tiempo de retardo (Lag) utilizado con el modelo Hec
Hms 4.0 (2010) fue calculando el tiempo de concentración por la fórmula de
Sheridan (1994) (Ecuación 4), considerando posteriormente que el Lag es igual a
0.6 * tiempo de concentración (Chow et al., 1994).
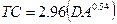 (4)
(4)
Siendo: TC (horas) = tiempo de concentración y DA =
área de drenaje en km2.
Análisis de los resultados
El criterio utilizado para determinar los mejores
resultados de CN y Ke calibrados, fue la utilización del coeficiente de Nash y
Sutcliffe (1970) (Ecuación 5):
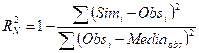 (5)
(5)
Siendo: Simi: Valores simulados; Obsi:
Valores observados; Mediaobs: Valor medio observado.
R2N puede variar entre – ∞ y 1. Un
valor R2N igual a 1 indica
una simulación perfecta (ajuste perfecto a la línea 1:1). Valores menores a
cero (negativos) indican que el error del modelo es mayor que la
variabilidad de la propiedad bajo estudio y por lo tanto es mejor usar el
promedio de los datos que utilizar los valores simulados.
La comparación de resultados obtenidos y el grado de
vinculación entre Ke y CN, se hicieron a partir de análisis de varianza,
correlación y regresión lineal. Para ello se utilizó
el programa InfoStat versión 2017 (Di Rienzo et al., 2017).
RESULTADOS Y DISCUSIÓN
Resultados generados con simulador de
lluvia
En la Tabla 1 se detallan los resultados medios de CN
y Ke y su variabilidad, calibrados a partir de los ensayos de simulación de
lluvia, junto con los de humedad gravimétrica inicial del suelo superficial.
Las tierras ganaderas presentaron una Ke significativamente
más baja (p<0.05), al mismo tiempo que un valor de CN mayor (p<0.05),
independientemente de la intensidad de lluvia aplicada. También se observó
cierto efecto de la intensidad de lluvia sobre estos parámetros, aunque el
mismo resultó significativo (p<0.05) únicamente para la Ke calibrada en las
tierras agrícolas. La variabilidad determinada para Ke fue sensiblemente
superior a la de CN, siendo a su vez el coeficiente de variación de este último
parámetro menor en las tierras ganaderas. La humedad edáfica inicial media fue
del 30-31%, salvo en el caso de las tierras agrícolas bajo 30 mm.h-1
de lluvia simulada, en las cuales el contenido hídrico del suelo fue
significativamente menor (p<0.05). Estos valores de contenido hídrico se
consideraron equivalentes a los de una condición antecedente de humedad media
(Condición II) (USDA-NRCS, 2010).
Tabla
1: Ke y CN medios calibrados y humedad edáfica superficial inicial.
|
Intensidad
lluvia
|
30 mm.h-1
|
60 mm.h-1
|
|
Aptitud
de las tierras
|
Agrícolas
|
Ganaderas
|
Agrícolas
|
Ganaderas
|
|
|
Media
|
CV (%)
|
Media
|
CV (%)
|
Media
|
CV (%)
|
Media
|
CV (%)
|
|
Ke
(mm h-1)
|
10.8 a A
|
71
|
1.7 b A
|
47
|
20.2 a B
|
73
|
2.2 b A
|
101
|
|
CN
|
76 b A
|
22
|
89 a A
|
17
|
78.2 b A
|
17
|
92 a A
|
5
|
|
HE
(%)
|
24 a B
|
23
|
30 b A
|
40
|
30 a A
|
15
|
31 a A
|
39
|
Ke: conductividad hidráulica
efectiva; CN: curva número; HE: humedad edáfica superficial inicial; CV:
coeficiente de variación. Letras minúsculas diferentes para una misma
propiedad, indican diferencias estadísticas significativas entre usos distintos
de la tierra para igual intensidad de lluvia (p<0.05). Letras mayúsculas
diferentes para una misma propiedad, indican diferencias estadísticas
significativas entre intensidades de lluvia distintas para igual uso de la
tierra (p<0.05).
En las tierras con aptitud ganadera,
independientemente de la intensidad de lluvia aplicada, se encontró una
vinculación débil entre los resultados de estos dos parámetros calibrados. Los
valores de CN se ubicaron mayoritariamente por encima de 85, mientras que los
de Ke oscilaron entre 0.2 y 6 mm.h-1. Estos resultados no difirieron
de lo encontrado en la bibliografía. En este sentido, Luque et al. (1979),
citados por Orsolini et al. (2000), mencionaron para suelos de ambientes bajos,
inundables y con escasa infiltración, valores de CN entre 84 y 88 para los
grupos hidrológicos de suelo C y D, respectivamente. Por su parte y de acuerdo
a lo publicado por Rawls et al. (1983), la Ke de los suelos con textura
superficial similar a los encontrados en el área evaluada (limosos y franco
limosos), sería en promedio 3.4 y 6.5 mm.h-1. Dada la falta de
vinculación entre ambos parámetros para este tipo de tierras, se prosiguió
únicamente con el análisis de dicha relación para las tierras con aptitud
agrícola.
En estas últimas se comprobó una relación negativa
entre ambos parámetros, la cual estuvo a su vez condicionada por la intensidad
de la lluvia aplicada (Figura 1), resultando mayor la Ke para un mismo valor de
CN cuando la precipitación fue de 60 mm.h-1. Sin embargo, para
valores de CN iguales o mayores a 85, la relación Ke-CN fue similar para ambas
intensidades de lluvia.
En este sentido y bajo 30 mm.h-1, para una
CN igual o mayor a 85, los resultados de Ke estuvieron dentro del rango 0.2-8
mm.h-1, mientras que para 60 mm.h-1 se registraron
valores de Ke en el rango de 0.7-9 mm.h-1. Este comportamiento
coincide con lo hallado para las tierras ganaderas: una Ke reducida para un
acotado intervalo de elevados valores de CN.
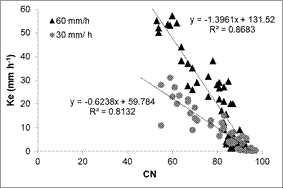
Figura 1. Relación
entre CN y Ke para las tierras con aptitud agrícola, considerando dos
intensidades de lluvia.
A su vez, la diferente sucesión de cultivos y la
posición en el paisaje, no modificaron la tendencia general encontrada para la
relación Ke-CN (Figuras 2 y 3) en las tierras agrícolas. Por su parte, los
resultados de estos dos parámetros no estuvieron condicionados por el diferente
uso de la tierra o por la posición en el paisaje de los suelos, dado que sus
valores abarcaron un rango similar, independientemente si los suelos se
ubicaban en la loma o media loma, o si se encontraban bajo el monocultivo de
soja o con una sucesión de cultivos más equilibrada con gramíneas.
La amplitud de resultados de la Ke y CN calibradas
para las tierras bajo agricultura, excedió lo publicado en la bibliografía.
Luque et al. (1979), citados por Orsolini et al. (2000), mencionan para suelos
pertenecientes al grupo hidrológico C, con cultivos de verano y bajo una
condición antecedente de humedad II, valores de CN entre 72 y 82, dependiendo
del grado de la pendiente del terreno. Por su parte y de acuerdo con Rawls et
al. (1983), la
Ke de estas tierras sería de igual magnitud a la
mencionada para las ganaderas, dada la similar textura superficial de ambos
tipos de suelo. De esta manera, los valores de Ke y CN citados por estos
autores, representarían entre el 10 y 23 % de los calibrados a partir de las
mediciones de infiltración realizadas a campo. Esta mayor variabilidad no pudo
ser explicada a partir del diferente contenido hídrico inicial de los suelos,
ya que el análisis de correlación mostró que el intervalo de humedad edáfica
registrado, no incidió significativamente sobre Ke y CN. Solo bajo 30 mm.h-1
de lluvia simulada, se comprobó una débil relación entre la humedad del suelo y
Ke (R2: 0.17).
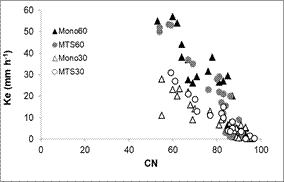
Figura 2. Relación
entre la CN y Ke para las tierras agrícolas, de acuerdo a la diferente sucesión
de cultivos.
Mono60
y Mono30: monocultivo de soja con 60 mm.h-1 y 30 mm.h-1
de lluvia aplicada, respectivamente. MTS60 y MTS30: rotación equilibrada de
gramíneas y leguminosas con 60 mm.h-1 y 30 mm.h-1 de
lluvia aplicada, respectivamente.
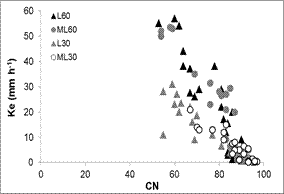
Figura 3. Relación
entre la CN y Ke para las tierras agrícolas, de acuerdo a la distinta posición
en el paisaje.
L60 y L30: Posición loma con 60 mm.h-1 y 30
mm.h-1 de lluvia aplicada, respectivamente. ML60 y ML30: Posición
media loma con 60 mm.h-1 y 30 mm.h-1 de lluvia aplicada,
respectivamente.
Distintos trabajos muestran que el tamaño del soporte
influye en la variabilidad de los resultados de conductividad hidráulica
saturada (Baveye y Spósito, 1984; Mallants et al., 1997). Por lo tanto, la
amplitud de valores observada en Ke y CN, obedecería en parte a que el reducido
tamaño de la parcela empleada en las mediciones de campo, habría capturado una
mayor diversidad de situaciones, las que habrían quedado diluidas si se hubiese
trabajado sobre una superficie mayor.
Los sistemas de producción agrícola en la región
Pampeana se encuentran bastante estandarizados, reduciendo la heterogeneidad de
las condiciones edáficas. Sin embargo, en el presente trabajo hubo factores que
no fueron identificados, que favorecieron el aumento en la variabilidad de los
parámetros que condicionan la relación lluvia-escurrimiento (CN y Ke). En este
sentido, algunos investigadores (Risse et al., 1995b; Zhang et al., 1995)
desarrollaron algunos algoritmos para predecir los cambios sufridos en la Ke, a
partir de modificaciones ocurridas en la estructura del suelo, la rugosidad
superficial, la intensidad del encostramiento superficial y el grado y tipo de
la cobertura vegetal.
Al aplicar la fórmula desarrollada por Nearing et al.
(1966) para suelos agrícolas, se comprobó una subestimación de la Ke respecto a
los valores calibrados de este parámetro (Figura 4).
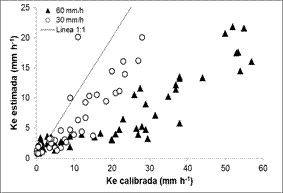
Figura 4. Relación
entre la Ke estimada de acuerdo a Nearing et al. (1966) y la Ke calibrada para
las tierras agrícolas.
Este comportamiento se observó con mayor intensidad en
los ensayos con 60 mm.h-1 de lluvia simulada. En este sentido, desde
valores muy bajos de la Ke calibrada y hasta los 30 mm.h-1 de este
parámetro, se observó un ligero incremento de la Ke estimada por fórmula. Sin
embargo, a partir de dicho valor se pudo comprobar una tendencia en los
resultados de la relación Ke estimada-Ke calibrada, bastante similar a la línea
de perfecto ajuste (1:1).
Por su parte, con una intensidad de lluvia de 30 mm.h-1,
si bien esta relación también se ubicó por debajo de la mencionada línea, la
distancia respecto a la misma fue menor.
Utilización del modelo Hec Hms 4.0 (2010)
La relación entre las láminas de escurrimiento
observadas a campo y estimadas por el modelo Hec Hms 4.0 para una superficie de
2 ha, dependió del parámetro empleado (CN o Ke) y de la intensidad de lluvia
aplicada (Figuras 5 y 6).
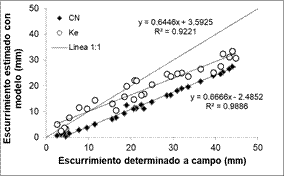
Figura 5. Relación
entre las láminas de escurrimiento generadas para ambas escalas bajo una
intensidad de lluvia de 60 mm.h-1.
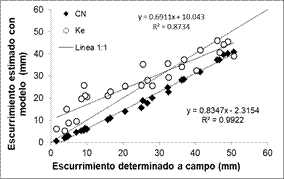
Figura 6. Relación
entre las láminas de escurrimiento generadas para ambas escalas bajo una
intensidad de lluvia de 30 mm.h-1.
Con una precipitación de 60 mm.h-1 (Figura
5) y para iguales valores de CN, el escurrimiento estimado por Hec Hms 4.0 fue
siempre menor al registrado en las parcelas del simulador de lluvia.
A su vez, este comportamiento se acentuó en la medida
que el escurrimiento fue mayor. Por su parte, los milímetros escurridos
estimados con dicho modelo al utilizar Ke, fueron bastante similares para ambas
escalas hasta una lámina de 12 mm, a partir de la cual las diferencias se
incrementaron. Al usar CN, los milímetros de escurrimiento estimados estuvieron
entre el 32 y 1577% por debajo de los registrados a campo (promedio: 51%),
mientras que utilizando Ke los valores extremos estuvieron por arriba (90%) y
por debajo (37%) de lo observado en las parcelas con menor superficie
(promedio: 11%).
El coeficiente de Nash y Sutcliffe (1970), obtenido al
contrastar los valores de escurrimiento para ambas escalas, fue 0.29 y 0.71 al
utilizar CN y Ke, respectivamente.
Con una precipitación de 30 mm.h-1 (Figura
6), los resultados estimados de escurrimiento a partir de CN presentaron un
comportamiento similar al observado con una intensidad de lluvia mayor, aunque
en este caso los porcentajes en que se redujo la lámina escurrida estimada con
el aumento de escala oscilaron entre el 17 y 75 % (promedio: 33%). Por su
parte, con Ke las mayores diferencias de estimación estuvieron entre -23% y
+276% (promedio: 46%). Para esta intensidad de lluvia, los resultados del
coeficiente de Nash y Sutcliffe (1970) obtenidos al comparar el escurrimiento
entre escalas, fueron muy similares al utilizar Ke o CN (0.82 y 0.80,
respectivamente).
De acuerdo con estos resultados, los valores de Ke y
CN calibrados serían diferentes de acuerdo a la superficie considerada. En este
sentido, Castiglioni (2016) determinó una reducción en la Ke calibrada del 60
al 100%, al pasar de una superficie de 0.25 m2 a otra de 2100 m2.
A su vez, este comportamiento dependería también de la intensidad de lluvia y
de la magnitud del escurrimiento generado (Figuras 5 y 6). Considerando los
coeficientes de Nash y Sutcliffe (1970) obtenidos, la utilización de la Ke
calibrada a una determinada escala, arrojaría menos incertidumbre al estimar el
escurrimiento a una escala mayor, en comparación al uso de la CN. No obstante,
para poder llegar a conclusiones más generales, sería necesario aportar más
resultados que abarquen una mayor diversidad de situaciones.
Estas diferencias no fueron suficientes para modificar
la relación CN-Ke previamente observada (Figuras 1, 7 y 8).
Estos parámetros,
calibrados mediante el modelo Hec Hms 4.0 con los datos de lámina de lluvia y
de escurrimiento obtenidos con el simulador de lluvia y transformados a caudal
para una superficie de 2 ha, mantuvieron dicha relación (Figura 1)
independientemente de la intensidad de lluvia aplicada (Figuras 7 y 8). Lo
mismo sucedió al calibrar la Ke mediante el mismo modelo, a partir de los
caudales estimados para una superficie de 2 ha con distintos valores de CN, no
estando estos directamente vinculados con los resultados obtenidos a campo
(Figuras 7 y 8).
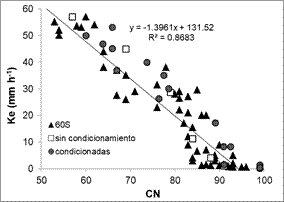
Figura 7. Relación
entre CN y Ke calibradas a dos escalas espaciales para una intensidad de 60
mm.h-1.
60S: Relación entre CN y Ke, generada a partir de los
ensayos de simulación de lluvia a campo; sin condicionamiento: Relación entre
CN y Ke, calibradas con el modelo Hec Hms 4.0 para una superficie de 2 ha, sin
estar los resultados condicionados por los caudales observados a campo;
condicionadas: Relación entre CN y Ke, calibradas con el modelo Hec Hms 4.0
para una superficie de 2 ha, estando los resultados condicionados por los
caudales observados a campo.
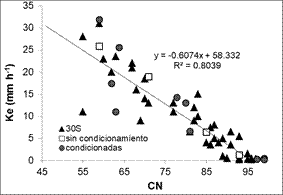
Figura 8. Relación
entre CN y Ke calibradas a dos escalas espaciales para una intensidad de 30
mm.h-1.
30S: Relación entre CN y Ke, generada a partir de los
ensayos de simulación de lluvia a campo; sin condicionamiento: Relación entre
CN y Ke, calibradas con el modelo Hec Hms 4.0 para una superficie de 2 ha, sin
estar los resultados condicionados por los caudales observados a campo;
condicionadas: Relación entre CN y Ke, calibradas con el modelo Hec Hms 4.0
para una superficie de 2 ha, estando los resultados condicionados por los
caudales observados a campo.
A su vez, el grado de dispersión obtenido de Ke y CN
no fue mayor que el determinado con las parcelas más pequeñas. Estos resultados
muestran la alta vinculación que existe entre la CN y Ke independientemente de
la escala, pudiendo por lo tanto la CN ser utilizada como una variable para
predecir Ke.
CONCLUSIONES
Con el objetivo de analizar la relación entre CN y Ke,
parámetros calibrados a partir de ensayos de infiltración realizados a campo
sobre suelos representativos de la Pampa Ondulada, se pudo comprobar en las
tierras con aptitud ganadera, que no existió una relación significativa entre
ambas variables. Sin embargo, en aquellos suelos con aptitud agrícola, se
observó una correlación lineal negativa y significativa entre CN y Ke, la que
fue afectada por la intensidad de lluvia aplicada. No obstante, para resultados
de CN superiores a 85, las diferencias en dicha relación entre intensidades de
lluvia se diluyeron. Los valores calibrados de estos parámetros, presentaron en
las tierras agrícolas una amplitud mayor que la publicada en la bibliografía.
La ecuación desarrollada por Nearing et al. (1996) subestimó los valores de Ke,
lo cual fue más evidente bajo una intensidad de lluvia de 60 mm.h-1.
La relación CN-Ke obtenida en pequeñas parcelas, se comportó de manera similar
al ser estimada para una superficie mayor, no obstante lo cual los resultados
obtenidos en el presente trabajo deberían ser convalidados con un mayor número
de ensayos y que abarquen una mayor diversidad de situaciones.
REFERENCIAS BIBLIOGRÁFICAS
Arnold, J. G., Srinivasan, R., Muttiah, R. S.,
Williams, J. R. (1998). Large area hydrologic modeling and assessment Part 1:
Model development. J.Am. Water Resour. As., 34(1), 73-89.
Baveye, P. y Sposito, G. (1984). The operational
significance of the continuum hypothesis in thetheory of wáter movement through
soils and aquifers. Water Resources Research, 20 (5), 521-530.
Castiglioni, M. (2016). Propiedades físicas y
conductividad hidráulica efectiva en el transcurso de una rotación trigo/soja. Cuadernos
del Curiham, 22, 15-25.
Chow, V. T., Maidment, D. R. y Mays, L. W. (1994).
Hidrología aplicada. Suárez, M. E. (Ed). McGraw Hill, Interamericana S.A., 584
págs.
Darder, M. L., Castiglioni, M., Andriulo, A. y Sasal,
M. C. (2018). Calibración de parámetros de un modelo de infiltración en la
cuenca alta del Arroyo
Pergamino. Ciencia del Suelo. En revisión.
De Roo, A. P. J. y Jetten, V. G. (1999). Calibrating
and validating the LISEM model for two data sets from the Netherlands and South
Africa. Catena, 37(3–4), 477–493.
Di Rienzo, J. A., Casanoves, F., Balzarini, M. G.,
Gonzalez, L., Tablada, M. y Robledo, C. W. (2017). InfoStat versión 2017. Grupo
InfoStat, FCA, Universidad Nacional de Córdoba, Argentina. URL http://www.infostat.com.ar
Ficklin, D. L. y Zhang, M. (2013). A comparison of the
curve number and Green-Ampt models in an agricultural watershed. Trans.
ASABE, 56(1), 61-69.
Green, W. H. y Ampt, G. (1911). Studies in soil
physics. I: The flow of air and water through soils. J. Agr. Sci., 4,
1–24.
Hawkins, R. (1993). Asymptotic determination of runoff
curve numbers from data. J. Irrig. Drainage Eng., 19(2), 334-345.
Hec-Hms 4.0. (2010). Hydologic Modeling
System. U.S. Army Corps of Engineers. Institute for Water Resource. Hydrologic
Engineering Center. Davis C.A.
Huber, W. C. y Dickinson, R. E. (1988). Storm Water
Management Model, Version 4: User's Manual. Environmental Research Laboratory.
U.S. Environmental Protection Agency, Athens, Georgia.
INTA. (1972). Cartas de Suelo de la República
Argentina. Hoja 3360-32 Pergamino, 106p.
Irurtia, C.B. y Mon, R. 1994.
Microsimulador de lluvia para determinar infiltración a campo. Instituto de
Suelos. CIRN INTA Castelar. Publicación Técnica 176.18 pp.
King, K. W., Arnold, J. G. y Bingner, R. L. (1999).
Comparison of Green-Ampt and curve number methods on Goodwin Creek watershed
using SWAT. Trans. ASAE., 42(4), 919-925.
Knisel, W. (1980). CREAMS. A Field-Scale Model for
Chemicals, Runoff and Erosion from Agricultural Management Systems. USDA
Conservation Research Report, No.26, 640 pp.
Laflen, J. M., Elliot, W. J., Flanagan, D. C., Meyer,
C. R. y Nearing, M. A. (1997). WEPP predicting water erosion using a
process-based model. J. Soil Water. Conserv., 52 (2), 96–102.
Lane, L. J. y Nearing, M. (Editors). (1989). USDA
Water Erosion Prediction Project: Hillslope Profile Model Documentation. NSERL
Report No. 2, National Soil Erosion Research Laboratory, West Lafayette,
Indiana.
Luque, J. A., Paoloni, J. D. y Bonorino, G. A. (1979).
Estudio geológico e hidrogeológico de la cuenca del Río Sauce Grande.
Publicación interna del Departamento de Ciencias Agrarias y de Ciencias
Naturales de la Universidad Nacional del Sur, Serie Hidrología. Bahía Blanca,
Argentina, 3: 64 p.
Mallants, D., Binayak, P., Mohanty, B. P., Vervoort,
A. y Feyen, J. (1997). Spatial analysis of saturated hydraulic conductivity in
a soil with macropores. Soil Technol., 10, 115-131.
Mao, L., Li, Y., Hao, W., Zhou, X., Xu, C. y Lei, T.
(2016). A new method to estimate soil water infiltration based on a modified
Green–Ampt model. Soil Till. Res., 161, 31–37.
Nash, J. E. y Sutcliffe, J. V. (1970). River Flow
Forecasting Through Conceptual Models, Part 1, A Discussion of Principles. J.
Hydrol., 10, 282-290.
Nearing, M. A., Deer-Ascough, L. y Laflen, J. M.
(1990). Sensitivity analysis of the WEPP hillslope profile erosion model. Trans.
ASAE, 33(3), 839-849.
Nearing, M. A., Liu, B. Y., Risse, L. M. y Zhang, X.
(1996). Curve numbers and Green-Ampt effective hydraulic conductivities. Water
Resour. Bull., 32(1), 125-136.
Orsolini, H. E., Zimmermann, E. D. y Basile, P. A.
(2000). Hidrología, procesos y métodos. UNR (Ed). Rosario. 319 pp.
Rawls, W. J. y Brakensiek, D. L. (1983). A procedure
to predict Green and Ampt infiltration parameters. In Proc. ASAE Conf. On
Advances in Infiltration, ASAE, St. Joseph, Michigan, pp. 102-112.
Rawls, W. J., Brakensiek, D. L. y Miller, N. (1983).
Green Ampt infiltration parameters from soils data. J Hidraul. Div., Am.
Soc. Civ. Eng., 109(1), 62-70.
Rawls, W. J. y Brakensiek, D. L. (1986). Comparison
Between Green-Ampt and Curve Number Runoff Predictions. Trans. ASAE,
29(6), 1597-1599.
Risse, L. M. (1994). Validation of WEPP Using Natural
Runoff Plot Data. Unpublished Ph.D. Dissertation, National Soil Erosion
Research Laboratory, Purdue University, West Lafayette, Indiana, 230 p.
Risse, L. M., Liu, B. Y. y Nearing, M. A. (1995a).
Using curve numbers to determine baseline values of Green-Ampt effective
hydraulic conductivities. Water Resour. Bull., 31(1), 147-158.
Risse, L. M., Nearing, M. A. y Zhang, X. C. (1995b).
Variability in Geen-Ampt effective hydraulic conductivity under fallow
conditions. J. Hydrol, 169, 1-24.
Sheridan, J. M. (1994). Hydrograph time parameters for
flatland watersheds. Trans. ASAE 37, 103-113.
USDA-NRCS. (2010). National Engineering
Handbook. Section 4: Hydrology. National Soil Conservation Service, USDA,
Washington, DC.
Van den Putte, A, Govers, G., Leys, A., Langhans, C.,
Clymans, W. y Diels, J. (2013). Estimating the parameters of the Green–Ampt
infiltration equation from rainfall simulation data: Why simpler is better. J.
Hydrol, 476, 332–344.
Van der Zweep, R. A. (1992). Evaluation of the Water
Erosion Prediction Project's Hydrologic Component on a Semi Arid Rangeland
Watershed. Unpublished M.S. Thesis, University of Arizona, Tucson, Arizona.
Yoo, K. H., Yoon, K. S. y Soileau, J. M. (1993).
Runoff curve numbers determined by three methods under conventional and
conservation tillage. Trans. ASAE, 36(1), 57-63.
Zhang, X. C.; Nearing, M. A. y Risse, L. M. (1995).
Estimation of Green-Ampt conductivity parameters: Part I. Row Crops. Trans.
ASAE, 38(4), 1069-1077.
REGISTRO BIBLIOGRÁFICO
Darder, M. L., Castiglioni, M., Andriulo,
A. y Nasal, M. C. (2018). Análisis de la relación entre la conductividad
hidráulica efectiva y la curva número bajo dos intensidades de lluvia. Cuadernos
del CURIHAM. 24, 1-10. DOI: 10.35305/curiham.v24i0.111
Tipo de Publicación: ARTICULO.
Trabajo recibido el 11/06/2018
y aprobado para su publicación el 30/11/2018.
![]() (1)
(1)![]() (2)
(2)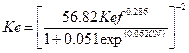 (3)
(3)![]()
![]() (4)
(4)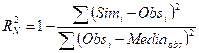 (5)
(5)






